2.3. Исследование вопросов применения непараметрических критериев согласия при проверке сложных гипотез.

            К наиболее используемым критериям согласия относятся непарамет­ри­че­ские критерии типа Колмогорова, типа  (Крамера-Мизеса-Смирнова) и  (Андерсона-Дарлинга) Мизеса.

В критерии Колмого­рова в качестве расстояния между эмпирическим и теоретическим законом ис­пользуется величина

,

где  – эмпирическая функция распределения,  – теоретическая функция распределения,  – объём выборки. В критериях типа  расстояние между гипотетическим и истинным рас­пределениями рассматривается в квадратичной метрике

,

где   - оператор математического ожидания.

            В случае простых гипотез предельные распределения статистик непара­мет­рических критериев типа Колмогорова,  и  Мизеса из­вестны давно и не зависят от вида наблюдаемого закона распределения и значений его параметров. Говорят, что эти критерии являются “свободными от рас­пределения”. Это дос­тоинство предопределяет широкое использование данных критериев в прило­жениях.

При проверке сложных гипотез, когда по той же самой выборке оценива­ются пара­метры наблюдаемого закона , непарамет­рические критерии согласия теряют свойство “свободы от распределения”.

Различия в предельных распределениях тех же самых статистик при про­верке простых и сложных гипотез очень существенны. Поэтому предостережения против неак­ку­ратного применения критериев со­гласия при проверке сложных гипотез неодно­кратно поднимались на страницах печати[1]. При проверке сложных гипотез на условный за­кон рас­пределения статистики  влияет целый ряд факторов, опреде­ляющих “сложность” гипотезы: вид наблюдаемого за­кона , соот­вет­ству­ющего истин­ной гипотезе ; тип оцениваемого пара­метра и коли­чество оцениваемых параметров; в некоторых ситуациях конкретное значение параметра (например, в случае гамма-рас­пре­деления); используемый метод оценивания параметров и точность вычисления оценок.

 

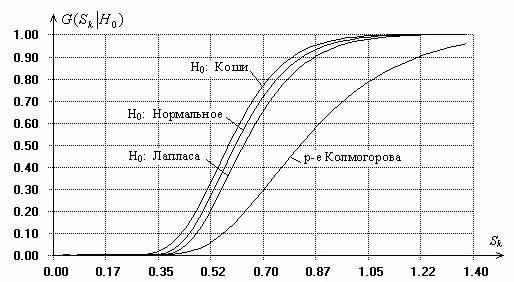
Рис. 1. Распределения статистики Колмогорова при проверке сложных гипотез о согласии с законами Лапласа, нормальным, Коши (ОМП 2-х параметров закона)

 

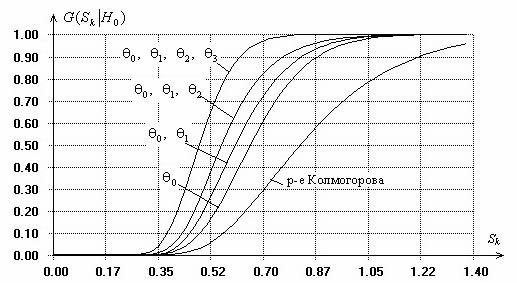
Рис. 2. Распределения статистики Колмогорова при проверке сложных гипотез о согласии с законом Su-Джонсона (при вычислении ОМП 1-го, 2-х, 3-х и 4х параметров закона)

 

Исходной точкой для исследований предельных распреде­лений статистик непарамет­рических критериев согласия при сложных гипоте­зах послужила работа Каса-Кифера-Вольфовица[2]. В литературных источниках изложен ряд подходов к использова­нию не­па­раметрических критериев согласия в случае проверки сложных гипотез. При достаточно большом объеме выборки ее можно разбить на две части и по од­ной из них оценивать параметры, а по другой проверять согласие[3]. В некоторых частных случаях предельные распределения статистик исследовались анали­ти­ческими методами[4], процентные точки распределений строились метода­ми статис­тического модели­рования[5]. Для при­ближенного вычисления веро­ятностей “согласия” вида  (достигаемого уровня значимости) стро­и­лись фор­мулы, дающие достаточно хорошие приближения при малых зна­че­ниях соответ­ствую­щих вероятностей[6]. В наших работах [11], [12], [13] иссле­до­вание распределений статистик непараметрических критериев согласия и по­строение моделей этих распределений осуществлялось с исполь­зованием мето­дики компьютерного анализа статистических законо­мерностей. Были по­строены модели распределений статистик при проверке согласия с параметрическими моделями. В [14] исследовалась возможность применения непараметрических критериев согласия для проверки адекватности непараметрических моделей.

Построенные в результате применения мето­дики модели предельных распределений статистик рассматриваемых критериев при проверке различных сложных гипотез и таблицы процентных точек послужили основой рекомендаций по стандартизации Р 50.1.037-2002 [15].

 

[Назад][Содержание][Вперед]

[1] Орлов А.И. // Заводская лаборатория. – 1985. – Т. 51. – №1. – С. 60-62.

[2] Kac M., Kiefer J., Wolfowitz J. // Ann. Math. Stat. – 1955. – V.26. – P.189-211.

[3] Durbin J. // Lect. Notes Math. – 1976. – V. 566. – P. 33–44.

[4] Мартынов Г.В. Критерии омега–квадрат. – М.: Наука, 1978. – 80 с.

[5]Pearson E.S., Hartley H.O. Biometrica tables for Statistics. V.2. – Cambridge: University Press, 1972. – 634 p.

Stephens M.A. // J. R. Stat. Soc. – 1970. – B. 32. – P. 115-122.

Stephens M.A. // J. Am. Statist. Assoc. – 1974. – V.69. – P. 730-737.

Chandra M., Singpurwalla N.D., Stephens M.A. // J. Am. Statist. Assoc. ­– 1981. – V.76. – P. 375.

[6] Тюрин Ю.Н. // Изв. АН СССР. Сер. Матем. – 1984. – Т. 48. – № 6. – C. 1314-1343.

Тюрин Ю.Н., Саввушкина Н.Е. // Изв. АН СССР. Сер. Техн. Кибернетика. – 1984. – № 3. – C. 109-112.

Саввушкина Н.Е. // Сб. тр. ВНИИ систем. исслед. – 1990, № 8.