2.2. Исследование вопросов применения критериев типа .

 

            При использовании критериев согласия типа  неоднозначность при построении и вычислении статистик

бывает связана с выбором числа интервалов и тем, каким образом область определения случайной величины разбивается на интервалы. Естественно, что такой произвол отражается на статистических свойствах применяемых критериев, в частности, на их мощности при различении близких конкурирующих гипотез. Очевидно, что выбор числа интервалов и способа разбиения на интервалы следует осуществлять с позиций обеспечения максимальной мощности критерия.

            Зависимость мощности от способа группирования.   Способ группирования оказывает особенно сильное влияние на мощность критериев типа . В работах [5] и [6] показано, что критерии согласия  Пирсона и отношения правдоподобия при проверке как простых, так и сложных гипотез имеют максимальную мощность против близких альтернатив, если использовать такое разбиение области определения случайной величины на интервалы, при котором потери в информации Фишера о параметрах закона, соответствующего проверяемой гипотезе , минимальны (асимптотически оптимальное группирование). В [7] для конкретных законов распределения представлен широкий состав построенных таблиц асимптотически оптимального группирования (АОГ-груп­пирования), минимизирующего потери в информации Фишера. Использование АОГ-груп­пирования при заданном числе интервалов обеспечивает максимальную мощность при близких гипотезах.

            Зависимость мощности от числа интервалов k. За всю историю применения критериев типа  была предложена не одна формула для выбора числа интервалов[1], но ни одна из представленных в различных рекомендациях не выводилась с позиций максимальной мощности применяемого критерия, а, в основном, исходя из близости плотности к ее непараметрической оценке, гистограмме. Зная предельные распределения  и  статистики , для любого заданного уровня значимости  можно оценить мощность соответствующего критерия, рассматривая её как функцию от числа интервалов k при заданном объеме выборки . Исследование мощности критериев типа  как функции от  и k проводилось методами статистического моделирования и аналитически [8].  Исследования показали, во-первых, что действительно с ростом k происходит падение мощности, что согласуется с результатами Чибисова[2] и Боровкова[3]. Во-вторых, для любой пары альтернатив и объема выборки существует оптимальное  k,  при котором мощность максимальна. Оптимальное число интервалов k зависит от объема выборки  и от конкретной пары конкурирующих гипотез  и . Чаще всего оптимальное k оказывается сущес­твенно меньше значений, рекомендуемых различными регламенти­рующи­ми документами и задаваемых множеством эмпирических формул.

 

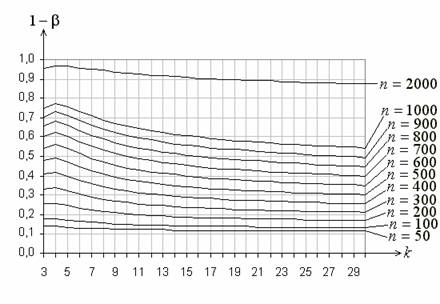
Рис. Функции мощности критерия  Пирсона при проверке простой гипотезы

о согласии с нормальным законом при равновероятном группировании

и альтернативе, соответствующей логистическому закону

 

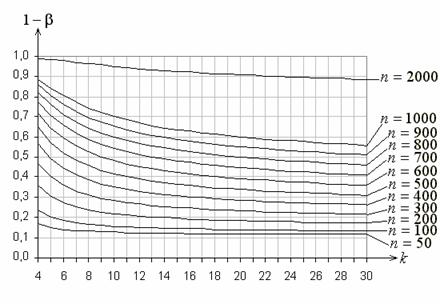
Рис. Функции мощности критерия  Пирсона при проверке сложной гипотезы

 о согласии с нормальным законом при равновероятном группировании

и альтернативе, соответствующей логистическому закону

 

Результаты исследований мощности критериев типа  от способа группирования и числа интервалов, таблицы асимптотически оптимального группирования составили основу рекомендаций по стандартизации Р 50.1.033-2001 [7]. Об ошибках и неверных действиях при использовании критериев типа   подробно изложено в [9].

 

[Назад][Содержание][Вперед]

[1] Новицкий П.В., Зограф И.А. Оценка погрешностей результатов из­ме­рений. - Л.: Энергоатомизд., 1991. - 303 с.

[2] Чибисов Д.М., Гванцеладзе Л.Г. // III сов.-яп. симп. по теор. Вер.. Ташкент: изд-во “Фан”, 1975. – С. 183-185.

[3] Боровков А.А. // Теория вероятностей и ее применение. 1977. Т. XXII. № 2. – С.375-378.