См. также: Прикладная
математическая статистика (материалы к семинарам)
Заводская лаборатория. Диагностика материалов. 2001. Т. 67. - № 1. - С. 52-64.
УДК 519.2
К ОЦЕНИВАНИЮ ПАРАМЕТРОВ НАДЕЖНОСТИ ПО ЦЕНЗУРИРОВАННЫМ ВЫБОРКАМ
Б.Ю.Лемешко, С.Я.Гильдебрант, С.Н.Постовалов
Новосибирский государственный технический университет
E-mail: headrd@fpm.ami.nstu.ru
Введение
Для определения параметров надежности по незавершенным испытаниям характерна ситуация, когда к моменту прекращения испытаний большой партии изделий наблюдается выход из строя лишь части из них, обычно достаточно малой по сравнению с объемом всей партии. В этом случае анализ приходится проводить по выборке, сильно цензурированной справа. Особенно часто приходится сталкиваться с задачей обработки цензурированных выборок, когда наблюдению оказывается доступной только часть области определения случайной величины, а для выборочных значений, попавших левее или правее этой области, фиксируется лишь сам факт этого попадания.
Очевидно, что в такой неполной (цензурированной) выборке содержится меньше
информации, чем в полной и это, естественно, отражается на точности оценивания
параметров аппроксимирующего закона распределения. При цензурировании
наблюдений снижается способность критериев согласия различать близкие законы
распределения. В этой связи оказывается интересным, насколько точно
можно оценить параметры наблюдаемого закона в зависимости от объема всей
выборки ![]() (объема партии) и величины наблюдаемой ее
части? Как отразится на точности оценивания наличие в неполной выборке
аномальных измерений и что дает в этом случае использование робастных оценок?
Как отразится на количестве сохранившейся в выборке информации и на точности
оценивания группирование наблюдаемой части неполной выборки? Ясно, что ответы
на эти вопросы зависят и от выбора параметрической модели наблюдаемого закона.
(объема партии) и величины наблюдаемой ее
части? Как отразится на точности оценивания наличие в неполной выборке
аномальных измерений и что дает в этом случае использование робастных оценок?
Как отразится на количестве сохранившейся в выборке информации и на точности
оценивания группирование наблюдаемой части неполной выборки? Ясно, что ответы
на эти вопросы зависят и от выбора параметрической модели наблюдаемого закона.
Толчком для проведения исследований (в основном численных, на моделируемых выборках), результаты которых излагаются в данной работе, послужила интересная на наш взгляд статья [1], в тексте которой, к сожалению, есть несколько опечаток, затрудняющих ее восприятие.
С точки зрения структуры данных цензурированные выборки являются частным случаем понятия частично группированной выборки, которую можно определить следующим образом [2].
Определение. Выборка называется частично
группированной, если имеющаяся в нашем распоряжении информация связана с
множеством непересекающихся интервалов, которые делят область определения
случайной величины на ![]() непересекающихся
интервалов граничными точками
непересекающихся
интервалов граничными точками
![]() ,
,
где
![]() - нижняя грань области определения случайной величины
- нижняя грань области определения случайной величины
![]() ,
, ![]() -
верхняя грань области определения случайной величины
-
верхняя грань области определения случайной величины ![]() , так, что каждый интервал принадлежит к одному из
двух типов:
, так, что каждый интервал принадлежит к одному из
двух типов:
а)
![]() -й интервал принадлежит к первому типу, если число
-й интервал принадлежит к первому типу, если число ![]() известно, но индивидуальные значения
известно, но индивидуальные значения ![]() неизвестны;
неизвестны;
б) ![]() -й
интервал принадлежит ко второму типу, если известно не только число
-й
интервал принадлежит ко второму типу, если известно не только число ![]() , но и все индивидуальные значения
, но и все индивидуальные значения ![]() .
.
В дальнейшем суммирование по интервалам первого и второго типов (аналогично
умножение) обозначается соответственно, как ![]() и
и ![]() .
.
Мы не будем акцентировать внимание на различии в цензурировании I-го и II-го типа, которое связано с условиями регистрации наблюдений, так как нет принципиальной разницы с точки зрения численной реализации оценивания параметров.
Количество информации Фишера как мера возможной точности оценивания
Наиболее универсальным методом по отношению к форме представления выборочных данных является метод максимального правдоподобия. В отличие от других метод позволяет находить оценки максимального правдоподобия (ОМП) параметров по негруппированным, частично группированным и группированным данным.
Вопросы существования ОМП по частично группированным выборкам, свойства таких оценок анализируются в [2]. Можно сказать, что частично группированная выборка является наиболее простым вариантом неполных выборок. Исследованию более сложных ситуаций неполных выборок посвящены работы [3-8]. Обширную библиографию работ по обработке цензурированных выборок можно найти в [7-8].
ОМП неизвестного параметра по частично группированным наблюдениям называется такое значение параметра, при котором функция правдоподобия
![]() ,
(1)
,
(1)
где
![]() - некоторая константа;
- некоторая константа; ![]() - функция плотности случайной величины;
- функция плотности случайной величины; 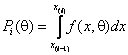 - вероятность попадания наблюдения в
- вероятность попадания наблюдения в ![]() -й интервал значений, достигает максимума на
множестве возможных значений параметра. При вычислении ОМП максимизируют (1)
или решают систему уравнений правдоподобия
-й интервал значений, достигает максимума на
множестве возможных значений параметра. При вычислении ОМП максимизируют (1)
или решают систему уравнений правдоподобия
![]() ,
(2)
,
(2)
где ![]() - размерность вектора параметров
- размерность вектора параметров ![]() .
.
В случае группированных или частично группированных данных система (2), за редким исключением, решается только численно. И хотя принципиальных трудностей нет, для ряда параметрических моделей законов, используемых в задачах надежности и контроля качества, попутно возникает необходимость в решении задач численного интегрирования, в том числе вычисления несобственных интегралов [9].
При выборке, цензурированной с двух сторон, являющейся частным случаем частично
группированной выборки, область определения случайной величины разбита на 3
интервала граничными точками ![]() так,
что значения левее
так,
что значения левее ![]() и правее
и правее ![]() не
наблюдаются. И система (2) принимает вид
не
наблюдаются. И система (2) принимает вид
![]() . (3)
. (3)
Если оценивается скалярный параметр, то асимптотическая дисперсия его ОМП определяется соотношением
![]() ,
(4)
,
(4)
где информационное количество Фишера определяется соотношением
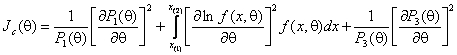 . (5)
. (5)
Если выборка цензурирована только справа, то в выражении исчезает левое слагаемое, только слева - правое слагаемое. Это соотношение позволяет судить о потерях информации о параметре распределения в зависимости от степени цензурирования слева или справа.
Об эффективности оценивания параметров по цензурированной выборке по отношению
к оцениванию по полной выборке можно судить по величине ![]() , где
, где ![]() –
количество информации Фишера в полной выборке. В табл. 1 приведены значения
–
количество информации Фишера в полной выборке. В табл. 1 приведены значения ![]() в зависимости от степени цензурирования для
распределений экспоненциального с плотностью
в зависимости от степени цензурирования для
распределений экспоненциального с плотностью ![]() , Вейбулла -
, Вейбулла - 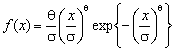 ,
нормального (логарифмически нормального) -
,
нормального (логарифмически нормального) - 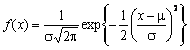 , Лапласа -
, Лапласа - ![]() ,
Рэлея -
,
Рэлея - 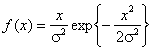 , гамма-распределения
, гамма-распределения ![]() . В случае векторного параметра в таблице приведены
значения отношения определителей соответствующих информационных матриц:
. В случае векторного параметра в таблице приведены
значения отношения определителей соответствующих информационных матриц: ![]() . В зависимости от закона цензурирование справа и
слева различным образом влияет на потери информации о параметрах. Так о
параметре экспоненциального распределения при той же степени цензурирования
слева в выборке сохраняется существенно больше информации, чем при цензурировании
справа. Это же характерно для распределения Вейбулла. В случае гамма-распределения
величина отношения
. В зависимости от закона цензурирование справа и
слева различным образом влияет на потери информации о параметрах. Так о
параметре экспоненциального распределения при той же степени цензурирования
слева в выборке сохраняется существенно больше информации, чем при цензурировании
справа. Это же характерно для распределения Вейбулла. В случае гамма-распределения
величина отношения ![]() зависит
от параметра формы
зависит
от параметра формы ![]() этого распределения и “перераспределяется”
между параметрами закона с его ростом. В табл. 1 ее значения для
гамма-распределения приведены для значений параметра формы 0.5 и 2.
этого распределения и “перераспределяется”
между параметрами закона с его ростом. В табл. 1 ее значения для
гамма-распределения приведены для значений параметра формы 0.5 и 2.
Таблица 1.
Отношение количества информации Фишера в наблюдении
цензурированной выборки к количеству информации в нецензурированной ![]()
![]()
|
Наблю- даемая |
О масштабном параметре распределений экспоненциального и Вейбулла |
О параметре формы распределения Вейбулла |
О двух параметрах распределения Вейбулла |
|||
|
часть % |
Цензурирование слева |
Цензурирование справа |
Цензурирование слева |
Цензурирование справа |
Цензурирование слева |
Цензурирование справа |
|
100 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
60 |
0.9914 |
0.6000 |
0.7091 |
0.4343 |
0.6389 |
0.2658 |
|
50 |
0.9805 |
0.5000 |
0.6343 |
0.4011 |
0.5256 |
0.1771 |
|
40 |
0.9597 |
0.4000 |
0.5680 |
0.3878 |
0.4076 |
0.1093 |
|
30 |
0.9212 |
0.3000 |
0.5168 |
0.3859 |
0.2878 |
0.0595 |
|
20 |
0.8476 |
0.2000 |
0.4883 |
0.3814 |
0.1707 |
0.0257 |
|
10 |
0.6891 |
0.1000 |
0.4830 |
0.3405 |
0.0654 |
0.0063 |
|
5 |
0.5223 |
0.0500 |
0.4654 |
0.2718 |
0.0234 |
0.0015 |
|
Наблю- даемая |
О параметре сдвига нормального распределения |
О параметре масштаба нормального распределения |
О двух параметрах нормального распределения |
О параметре масштаба распределения Лапласа |
О параметре распределения Рэлея |
|
|
часть % |
Цензурирование слева*) |
Цензурирование слева*) |
Цензурирование слева*) |
Цензурирование слева*) |
Цензурирование слева |
Цензурирование справа |
|
100 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
60 |
0.8753 |
0.5599 |
0.4399 |
0.6131 |
0.9914 |
0.6000 |
|
50 |
0.8183 |
0.5000 |
0.3296 |
0.6103 |
0.9805 |
0.5000 |
|
40 |
0.7467 |
0.4601 |
0.2311 |
0.5918 |
0.9597 |
0.4000 |
|
30 |
0.6550 |
0.4399 |
0.1457 |
0.5538 |
0.9212 |
0.3000 |
|
20 |
0.5336 |
0.4309 |
0.0754 |
0.4885 |
0.8476 |
0.2000 |
|
10 |
0.3591 |
0.4252 |
0.0239 |
0.3740 |
0.6891 |
0.1000 |
|
5 |
0.2318 |
0.3795 |
0.0073 |
0.2730 |
0.5223 |
0.0500 |
|
Наблю- даемая |
О параметре формы
гамма-распределения ( |
О параметре
масштаба гамма-распределения ( |
О двух параметрах
гамма-распределения ( |
|||
|
часть % |
Цензурирование слева |
Цензурирование справа |
Цензурирование слева |
Цензурирование справа |
Цензурирование слева |
Цензурирование справа |
|
100 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
60 |
0.6693 |
0.9698 |
0.9984 |
0.4750 |
0.4756 |
0.3201 |
|
50 |
0.5819 |
0.9484 |
0.9955 |
0.3715 |
0.3589 |
0.2163 |
|
40 |
0.4902 |
0.9157 |
0.9876 |
0.2778 |
0.2522 |
0.1343 |
|
30 |
0.3927 |
0.8646 |
0.9681 |
0.1939 |
0.1586 |
0.0730 |
|
20 |
0.2865 |
0.7796 |
0.9208 |
0.1196 |
0.0812 |
0.0311 |
|
10 |
0.1651 |
0.6192 |
0.7925 |
0.0554 |
0.0251 |
0.0075 |
|
5 |
0.0935 |
0.4615 |
0.6321 |
0.0265 |
0.0076 |
0.0018 |
|
Наблю- даемая |
О параметре формы
гамма-распределения ( |
О параметре масштаба
гамма-распределения ( |
О двух параметрах гамма-распределения
( |
|||
|
часть % |
Цензурирование слева |
Цензурирование справа |
Цензурирование слева |
Цензурирование справа |
Цензурирование слева |
Цензурирование справа |
|
100 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
60 |
0.7770 |
0.9353 |
0.9759 |
0.6895 |
0.4395 |
0.4171 |
|
50 |
0.7022 |
0.8985 |
0.9548 |
0.5981 |
0.3284 |
0.3071 |
|
40 |
0.6168 |
0.8475 |
0.9208 |
0.5005 |
0.2296 |
0.2108 |
|
30 |
0.5177 |
0.7758 |
0.8659 |
0.3957 |
0.1444 |
0.1292 |
|
20 |
0.3993 |
0.6697 |
0.7737 |
0.2815 |
0.0749 |
0.0642 |
|
10 |
0.2483 |
0.4955 |
0.6002 |
0.1543 |
0.0248 |
0.0190 |
|
5 |
0.1498 |
0.3470 |
0.4369 |
0.0825 |
0.0089 |
0.0054 |
*) – при левом и правом цензурировании ситуация идентична.
Если задаться максимально допустимой асимптотической дисперсией, величина которой определяется соотношением (4), то в зависимости от степени цензурирования можно оценить минимально необходимый объем выборки, при котором она должна быть не хуже заданной. Или, наоборот, по объему выборки оценить максимально возможную степень цензурирования, еще обеспечивающую требуемую точность оценивания.
Например, результаты исследования точности вычисления ОМП параметров распределения Вейбулла в зависимости от степени цензурирования справа или слева показали, что, так как при той же степени цензурирования слева в выборке сохраняется больше информации о параметрах распределения, то это положительно сказывается и на точности оценивания.
Аналогичные результаты по оцениванию по цензурированным выборкам ОМП одновременно двух параметров логарифмически нормального распределения подтвердили, что, так как потери информации одинаковы при одной и той же степени цензурирования слева и справа, то это одинаково отражается и на точности оценивания параметров нормального и логарифмически нормального распределений.
Асимптотическая дисперсия является теоретической характеристикой точности оценивания. Реально же точность оценивания (дисперсия оценки) не в последнюю очередь зависит от особенностей случайной выборки (от возможного наличия в ней аномальных наблюдений, от того, действительно ли наблюдаемая выборка принадлежит предполагаемому закону).
Экспериментальные оценки точности оценивания по цензурированным выборкам
Реальную картину того, насколько точно можно оценить параметры закона по
цензурированной выборке в зависимости от объема полной выборки ![]() дают результаты исследования методами
статистического моделирования, представленные в таблицах 2-7. Количество
дают результаты исследования методами
статистического моделирования, представленные в таблицах 2-7. Количество ![]() моделируемых выборок, по которым исследовались
законы распределения оценок по выборкам объема
моделируемых выборок, по которым исследовались
законы распределения оценок по выборкам объема ![]() , во всех рассматриваемых в дальнейшем случаях было
взято равным 1000. В табл. 2 приведены полученные значения отношения дисперсии
ОМП параметра масштаба экспоненциального распределения по полной выборке
, во всех рассматриваемых в дальнейшем случаях было
взято равным 1000. В табл. 2 приведены полученные значения отношения дисперсии
ОМП параметра масштаба экспоненциального распределения по полной выборке ![]() к дисперсии ОМП по цензурированной
к дисперсии ОМП по цензурированной ![]() при различной степени цензурирования (различной
величине наблюдаемой части выборки) и различном объеме полной выборки
при различной степени цензурирования (различной
величине наблюдаемой части выборки) и различном объеме полной выборки ![]() :
: ![]() (относительная
эффективность оценивания). При построении распределений оценок моделировались
выборки по экспоненциальному закону с параметром масштаба
(относительная
эффективность оценивания). При построении распределений оценок моделировались
выборки по экспоненциальному закону с параметром масштаба ![]() . Находилась оценка по полной выборке, и по той же
самой, но предварительно цензурированной выборке.
. Находилась оценка по полной выборке, и по той же
самой, но предварительно цензурированной выборке.
Таблица 2.
Относительная эффективность оценивания параметра
экспоненциального распределения по цензурированным выборкам по сравнению с
оцениванием по полной выборке ![]() в зависимости от объема выборки n
в зависимости от объема выборки n
|
Наблю-даемая часть |
n = 2000 |
n = 1000 |
n = 500 |
|||
|
|
Цензуриро-вание слева |
Цензуриро-вание справа |
Цензуриро-вание слева |
Цензуриро-вание справа |
Цензуриро-вание слева |
Цензуриро-вание справа |
|
100% |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
|
60% |
1,0358 |
0,6677 |
0,9558 |
0,5899 |
0,9342 |
0,6806 |
|
50% |
1,0159 |
0,5193 |
0,9706 |
0,5164 |
0,9794 |
0,5598 |
|
40% |
1,0611 |
0,4310 |
0,9907 |
0,4179 |
0,9084 |
0,4441 |
|
30% |
1,0009 |
0,3249 |
0,9413 |
0,2829 |
0,8986 |
0,3118 |
|
20% |
0,9166 |
0,2050 |
0,8629 |
0,1983 |
0,7497 |
0,2235 |
|
10% |
0,6972 |
0,0992 |
0,6952 |
0,0884 |
0,6950 |
0,0957 |
|
5% |
0,5618 |
0,0555 |
0,5204 |
0,0456 |
0,5089 |
0,0457 |
|
Наблю-даемая часть |
n = 300 |
n = 200 |
n = 100 |
|||
|
|
Цензуриро-вание слева |
Цензуриро-вание справа |
Цензуриро-вание слева |
Цензуриро-вание справа |
Цензуриро-вание слева |
Цензуриро-вание справа |
|
100% |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
|
60% |
1,0460 |
0,5326 |
0,9699 |
0,4984 |
0,9623 |
0,6078 |
|
50% |
1,0181 |
0,4729 |
0,9886 |
0,4171 |
0,9367 |
0,5084 |
|
40% |
0,9755 |
0,3675 |
0,9978 |
0,3449 |
0,9401 |
0,3833 |
|
30% |
0,9652 |
0,2979 |
0,9468 |
0,2332 |
0,8670 |
0,2848 |
|
20% |
0,8841 |
0,2051 |
0,8578 |
0,1684 |
0,8204 |
0,1691 |
|
10% |
0,7386 |
0,0932 |
0,6985 |
0,0783 |
0,6533 |
0,0582 |
|
5% |
0,5676 |
0,0395 |
0,5349 |
0,0328 |
0,4847 |
0,0191 |
Таблица 3.
Относительная эффективность оценивания двух параметров
нормального распределения по цензурированным выборкам по сравнению с
оцениванием по полной выборке ![]() в зависимости от объема выборки n
в зависимости от объема выборки n
|
Наблю-даемая часть |
n = 2000 |
n = 1000 |
n = 500 |
n = 300 |
n = 200 |
n = 100 |
|
|
Цензуриро-вание слева |
Цензуриро-вание слева |
Цензуриро-вание слева |
Цензуриро-вание слева |
Цензуриро-вание слева |
Цензуриро-вание слева |
|
100% |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
|
60% |
0,4326 |
0,4200 |
0,5000 |
0,4219 |
0,4020 |
0,4045 |
|
50% |
0,3144 |
0,2945 |
0,3615 |
0,2913 |
0,3439 |
0,2967 |
|
40% |
0,2259 |
0,2368 |
0,2646 |
0,2269 |
0,2212 |
0,2119 |
|
30% |
0,1298 |
0,1412 |
0,1677 |
0,1345 |
0,1298 |
0,1348 |
|
20% |
0,0674 |
0,0734 |
0,0835 |
0,0713 |
0,0793 |
0,0601 |
|
10% |
0,0237 |
0,0252 |
0,0248 |
0,0269 |
0,0253 |
0,0210 |
|
5% |
0,0077 |
0,0067 |
0,0087 |
0,0071 |
0,0073 |
0,0082 |
Если сравнить полученные на основании моделирования и приведенные в табл. 2 оценки значений относительной эффективности со значениями асимптотической эффективности из соответствующих колонок табл. 1, то увидим, что результаты моделирования в целом подтверждают результаты, представленные в табл. 1. В колонках табл. 2 и 3 содержатся значения большие и меньшие соответствующих теоретических значений из табл. 1 (как и положено оценкам). В некоторых случаях, когда асимптотическая эффективность близка к 1 (при малых потерях информации), её оценки (значения относительной эффективности оценивания) могут оказаться и иногда оказываются больше 1 (например, теоретическая – 0.9914, выборочная – 1.0358, см. табл. 1 и 2). Это объясняется тем, что ОМП по цензурированным выборкам обладают большей устойчивостью (давно известный и используемый на практике факт). И те отклонения в выборке, которые повлияли на ОМП по полной выборке, могут не повлиять на ОМП по цензурированной (если они попали в ненаблюдаемую область). Именно поэтому выборочная дисперсия ОМП по полным выборкам может оказаться (и иногда оказывается) больше выборочной дисперсии ОМП по цензурированным (при условии близости соответствующих асимптотических дисперсий).
Сравнивая значения, представленные в табл. 2, с
соответствующими значениями асимптотической эффективности для экспоненциального
закона при цензурировании слева и справа, приведенными в табл. 1, можно судить
о возможной точности оценивания по соответствующей части наблюдаемой выборки в
зависимости от объема полной выборки ![]() .
.
На рис. 1-2 представлены построенные плотности оценок ![]() и
и ![]() параметра
масштаба экспоненциального закона для
параметра
масштаба экспоненциального закона для ![]() =2000
и
=2000
и ![]() =100 при различной степени цензурирования справа. С
уменьшением
=100 при различной степени цензурирования справа. С
уменьшением ![]() и увеличением степени цензурирования
увеличивается асимметрия закона распределения
и увеличением степени цензурирования
увеличивается асимметрия закона распределения ![]() .
.
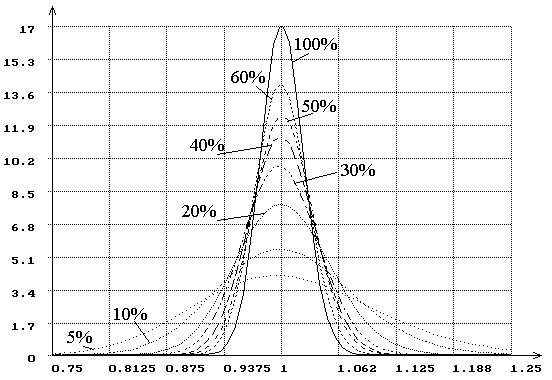
Рис.1. Плотности распределения оценок масштабного параметра экспоненциального
распределения при цензурировании справа при различной величине (%) наблюдаемой
области определения случайной величины и полном объеме
выборки ![]() =2000.
=2000.
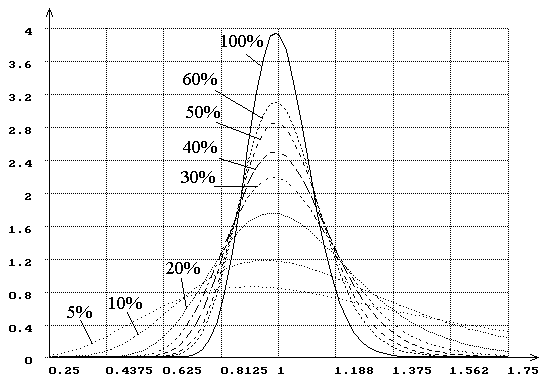
Рис.2. Плотности распределения оценок масштабного параметра экспоненциального
распределения при цензурировании справа при различной величине (%) наблюдаемой
области определения случайной величины и полном объеме
выборки ![]() =100.
=100.
Табл. 3, аналогично табл. 2, характеризует полученные в результате
статистического моделирования значения относительной эффективности оценивания
по цензурированным выборкам двух параметров нормального закона в зависимости от
![]() . В таблице приведены значения
. В таблице приведены значения ![]() (сравните с соответствующими значениями
эффективности, представленными в табл. 1). Рис. 3-4 иллюстрируют законы
распределения оценок
(сравните с соответствующими значениями
эффективности, представленными в табл. 1). Рис. 3-4 иллюстрируют законы
распределения оценок ![]() и
и
![]() параметров нормального закона при различной степени
цензурирования слева. При цензурировании справа для распределений оценок
параметров нормального закона при различной степени
цензурирования слева. При цензурировании справа для распределений оценок ![]() имеем картину зеркального отражения по
отношению к распределениям, представленным на рис. 3.
имеем картину зеркального отражения по
отношению к распределениям, представленным на рис. 3.
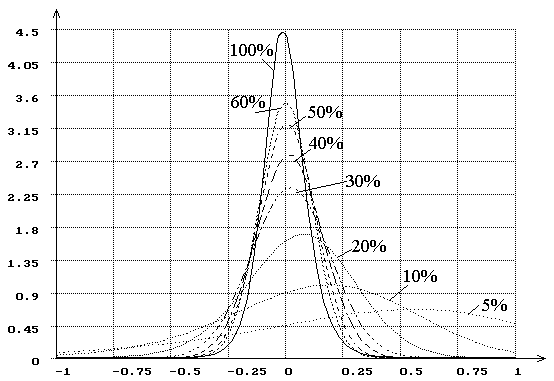
Рис.3. Плотности распределения оценок параметра сдвига нормального
распределения при цензурировании слева при различной величине (%) наблюдаемой
области определения случайной величины и объеме
выборки ![]() =100.
=100.
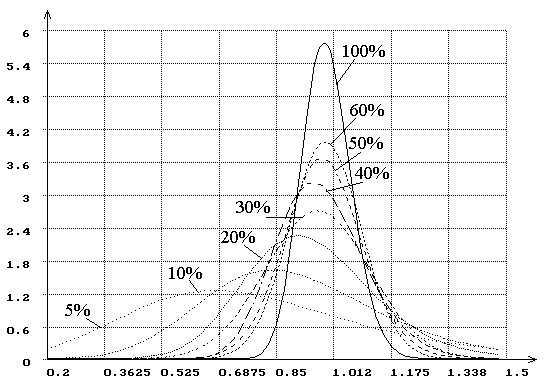
Рис.4. Плотности распределения оценок масштабного параметра нормального
распределения при цензурировании слева (справа) при
различной величине (%) наблюдаемой области определения случайной величины и
объеме выборки ![]() =100.
=100.
В целях определения возможной точности оценивания параметров по цензурированным
выборкам исследовались распределения величин вида ![]() . Результаты показали, что эти распределения при малых
. Результаты показали, что эти распределения при малых
![]() и большой степени цензурирования оказываются
существенно асимметричными. На рис. 5 приведены распределения величины
и большой степени цензурирования оказываются
существенно асимметричными. На рис. 5 приведены распределения величины ![]() для масштабного параметра экспоненциального
закона при объеме выборки
для масштабного параметра экспоненциального
закона при объеме выборки ![]() =100.
В таблицах 4-5 приведены значения выборочных среднего
=100.
В таблицах 4-5 приведены значения выборочных среднего ![]() и среднеквадратического отклонения
и среднеквадратического отклонения ![]() величин
величин ![]() в
случае экспоненциального закона при различном объеме выборок и различной
степени цензурировании слева и справа. Приводимые в таблицах значения
в
случае экспоненциального закона при различном объеме выборок и различной
степени цензурировании слева и справа. Приводимые в таблицах значения ![]() позволяют судить о смещении оценок
позволяют судить о смещении оценок ![]() , а значения
, а значения ![]() –
о их точности. Анализируя результаты, можно отметить, что если при
цензурировании слева оценки
–
о их точности. Анализируя результаты, можно отметить, что если при
цензурировании слева оценки ![]() параметра
масштаба экспоненциального закона практически несмещенные, то при
цензурировании справа они оказываются существенно смещенными вправо. Причем
смещение растет с уменьшением наблюдаемой части выборки и уменьшением полного
объема выборки.
параметра
масштаба экспоненциального закона практически несмещенные, то при
цензурировании справа они оказываются существенно смещенными вправо. Причем
смещение растет с уменьшением наблюдаемой части выборки и уменьшением полного
объема выборки.
Таблица 4.
Точность оценивания параметра
экспоненциального закона по цензурированной слева выборке (параметры
нормального закона, аппроксимирующего распределение величин ![]() )
)
|
Наблюдаемая часть |
n = 2000 |
n = 1000 |
n = 500 |
|||
|
|
|
|
|
|
|
|
|
60% |
0,0001 |
0,0020 |
0,0000 |
0,0031 |
0,0000 |
0,0042 |
|
50% |
-0,0002 |
0,0032 |
0,0000 |
0,0045 |
0,0000 |
0,0064 |
|
40% |
-0,0001 |
0,0048 |
0,0004 |
0,0063 |
0,0001 |
0,0092 |
|
30% |
-0,0002 |
0,0063 |
-0,0004 |
0,0093 |
-0,0004 |
0,0131 |
|
20% |
-0,0006 |
0,0094 |
0,0004 |
0,0136 |
-0,0003 |
0,0193 |
|
10% |
0,0001 |
0,0149 |
0,0003 |
0,0209 |
0,0003 |
0,0301 |
|
5% |
-0,0009 |
0,0213 |
-0,0007 |
0,0305 |
-0,0011 |
0,0427 |
|
Наблюдаемая часть |
n = 300 |
n = 200 |
n = 100 |
|||
|
|
|
|
|
|
|
|
|
60% |
0,0000 |
0,0052 |
0,0000 |
0,0067 |
0,0006 |
0,0098 |
|
50% |
0,0000 |
0,0083 |
0,0001 |
0,0098 |
-0,0001 |
0,0145 |
|
40% |
0,0000 |
0,0117 |
0,0003 |
0,0150 |
-0,0002 |
0,0207 |
|
30% |
-0,0008 |
0,0164 |
-0,0008 |
0,0214 |
-0,0019 |
0,0300 |
|
20% |
0,0005 |
0,0251 |
-0,0002 |
0,0300 |
0,0007 |
0,0436 |
|
10% |
-0,0026 |
0,0370 |
0,0031 |
0,0481 |
-0,0023 |
0,0706 |
|
5% |
0,0006 |
0,0567 |
0,0010 |
0,0662 |
0,0021 |
0,0953 |
Таблица 5.
Точность оценивания параметра
экспоненциального закона по цензурированной справа выборке (параметры нормального
закона, аппроксимирующего распределение величин ![]() )
)
|
Наблюдаемая часть |
n = 2000 |
n = 1000 |
n = 500 |
||||
|
|
|
|
|
|
|
|
|
|
60% |
0,0005 |
0,0178 |
0,0000 |
0,0252 |
-0,0023 |
0,0362 |
|
|
50% |
0,0000 |
0,0219 |
-0,0009 |
0,0309 |
-0,0025 |
0,0455 |
|
|
40% |
-0,0020 |
0,0277 |
-0,0033 |
0,0401 |
-0,0012 |
0,0544 |
|
|
30% |
0,0014 |
0,0359 |
-0,0026 |
0,0465 |
-0,0048 |
0,0667 |
|
|
20% |
-0,0003 |
0,0445 |
-0,0059 |
0,0648 |
-0,0073 |
0,0869 |
|
|
10% |
-0,0092 |
0,0682 |
-0,0080 |
0,0946 |
-0,0198 |
0,1353 |
|
|
5% |
-0,0109 |
0,1025 |
-0,0212 |
0,1425 |
-0,0415 |
0,2116 |
|
|
Наблюдаемая часть |
n = 300 |
n = 200 |
n = 100 |
||||
|
|
|
|
|
|
|
|
|
|
60% |
-0,0008 |
0,0460 |
-0,0046 |
0,0605 |
-0,0088 |
0,0831 |
|
|
50% |
-0,0035 |
0,0574 |
-0,0046 |
0,0693 |
-0,0079 |
0,1078 |
|
|
40% |
-0,0039 |
0,0719 |
-0,0078 |
0,0898 |
-0,0137 |
0,1254 |
|
|
30% |
-0,0109 |
0,0914 |
-0,0120 |
0,1099 |
-0,0357 |
0,1716 |
|
|
20% |
-0,0120 |
0,1207 |
-0,0186 |
0,1471 |
-0,0376 |
0,2162 |
|
|
10% |
-0,0211 |
0,1788 |
-0,0519 |
0,2331 |
-0,1022 |
0,3762 |
|
|
5% |
-0,0676 |
0,2865 |
-0,1170 |
0,3831 |
-0,2221 |
0,6734 |
|
|
|
|
|
|
|
|
|
|
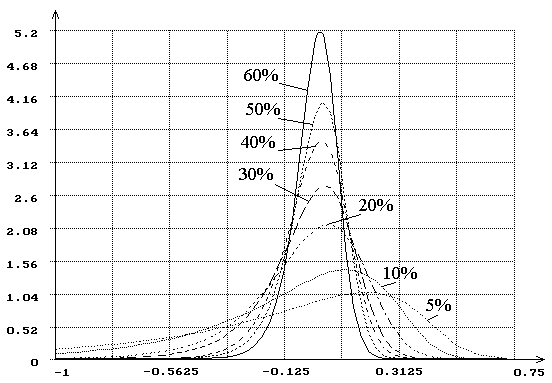
Рис.5. Плотности распределения величины ![]() для оценок масштабного параметра
экспоненциального закона при цензурировании справа при различной величине (%)
наблюдаемой области определения случайной величины и объеме выборки
для оценок масштабного параметра
экспоненциального закона при цензурировании справа при различной величине (%)
наблюдаемой области определения случайной величины и объеме выборки ![]() =100.
=100.
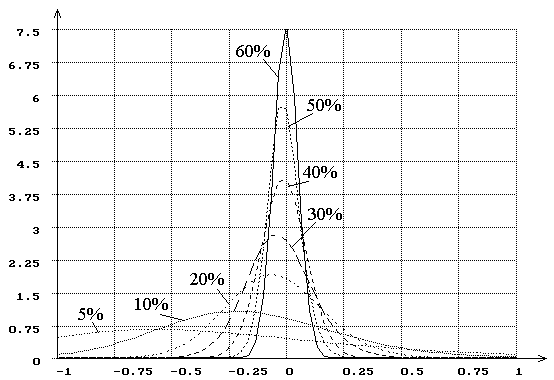
Рис. 6. Плотности распределения величины ![]() для оценок параметра сдвига нормального закона
при цензурировании слева при различной величине (%) наблюдаемой области
определения случайной величины и объеме выборки
для оценок параметра сдвига нормального закона
при цензурировании слева при различной величине (%) наблюдаемой области
определения случайной величины и объеме выборки ![]() =100.
=100.
В табл. 6-7 представлены результаты, полученные при исследовании точности
оценивания параметров нормального закона (величин ![]() и
и ![]() )
по цензурированной слева выборке. В приводимых таблицах представлены значения
выборочного среднего
)
по цензурированной слева выборке. В приводимых таблицах представлены значения
выборочного среднего ![]() и
среднеквадратического отклонения
и
среднеквадратического отклонения ![]() для
величин
для
величин ![]() и
и ![]() .
Как видим, в данном случае с уменьшением наблюдаемой части выборки и
уменьшением объема выборки
.
Как видим, в данном случае с уменьшением наблюдаемой части выборки и
уменьшением объема выборки ![]() увеличивается
смещение обеих оценок
увеличивается
смещение обеих оценок ![]() и
и
![]() и увеличивается дисперсия этих оценок. При этом
цензурирование слева приводит к смещению оценки параметра сдвига вправо, а
цензурирование справа – к смещению оценки параметра сдвига влево. Для параметра
масштаба нормального распределения цензурирование слева или справа приводит к
смещению оценки параметра масштаба влево. На рис. 6 приведены распределения
величины
и увеличивается дисперсия этих оценок. При этом
цензурирование слева приводит к смещению оценки параметра сдвига вправо, а
цензурирование справа – к смещению оценки параметра сдвига влево. Для параметра
масштаба нормального распределения цензурирование слева или справа приводит к
смещению оценки параметра масштаба влево. На рис. 6 приведены распределения
величины ![]() для параметра сдвига нормального закона при
объеме выборки
для параметра сдвига нормального закона при
объеме выборки ![]() =100. В данном случае распределения обладают большей
симметрией.
=100. В данном случае распределения обладают большей
симметрией.
Таблица 6.
Точность оценивания параметра сдвига при оценивании
двух параметров нормального распределения по цензурированной слева выборке
(параметры нормального закона, аппроксимирующего распределение величин ![]() )
)
|
Наблюдаемая часть |
n = 2000 |
n = 1000 |
n = 500 |
|||
|
|
|
|
|
|
|
|
|
60% |
-0,0001 |
0,0001 |
-0,0007 |
0,0003 |
-0,0006 |
0,0006 |
|
50% |
-0,0006 |
0,0002 |
-0,0012 |
0,0005 |
-0,0024 |
0,0010 |
|
40% |
-0,0002 |
0,0005 |
-0,0020 |
0,0010 |
-0,0014 |
0,0019 |
|
30% |
-0,0013 |
0,0010 |
-0,0017 |
0,0021 |
-0,0029 |
0,0038 |
|
20% |
-0,0005 |
0,0024 |
-0,0065 |
0,0047 |
-0,0096 |
0,0101 |
|
10% |
-0,0087 |
0,0080 |
-0,0189 |
0,0172 |
-0,0262 |
0,0315 |
|
5% |
-0,0310 |
0,0239 |
-0,0435 |
0,0435 |
-0,0713 |
0,0933 |
|
Наблюдаемая часть |
n = 300 |
n = 200 |
n = 100 |
|||
|
|
|
|
|
|
|
|
|
60% |
-0,0017 |
0,0008 |
-0,0030 |
0,0014 |
-0,0037 |
0,0027 |
|
50% |
-0,0044 |
0,0017 |
-0,0064 |
0,0027 |
-0,0104 |
0,0050 |
|
40% |
-0,0072 |
0,0034 |
-0,0047 |
0,0054 |
-0,0130 |
0,0098 |
|
30% |
-0,0106 |
0,0067 |
-0,0168 |
0,0097 |
-0,0278 |
0,0220 |
|
20% |
-0,0165 |
0,0170 |
-0,0299 |
0,0227 |
-0,0503 |
0,0455 |
|
10% |
-0,0586 |
0,0552 |
-0,0775 |
0,0837 |
-0,1551 |
0,1515 |
|
5% |
-0,1295 |
0,1523 |
-0,2264 |
0,2465 |
-0,3390 |
0,4480 |
Таблица 7.
Точность оценивания параметра масштаба
при оценивании двух параметров нормального распределения по цензурированной слева
выборке (параметры нормального закона, аппроксимирующего распределение величин ![]() )
)
|
Наблюдаемая часть |
n = 2000 |
n = 1000 |
n = 500 |
|||
|
|
|
|
|
|
|
|
|
60% |
0,0002 |
0,0003 |
0,0010 |
0,0005 |
0,0009 |
0,0010 |
|
50% |
0,0006 |
0,0004 |
0,0012 |
0,0007 |
0,0022 |
0,0014 |
|
40% |
0,0003 |
0,0006 |
0,0023 |
0,0011 |
0,0009 |
0,0022 |
|
30% |
0,0012 |
0,0008 |
0,0010 |
0,0018 |
0,0026 |
0,0033 |
|
20% |
0,0004 |
0,0015 |
0,0050 |
0,0030 |
0,0066 |
0,0064 |
|
10% |
0,0060 |
0,0034 |
0,0116 |
0,0073 |
0,0148 |
0,0132 |
|
5% |
0,0156 |
0,0071 |
0,0223 |
0,0131 |
0,0386 |
0,0280 |
|
Наблюдаемая часть |
n = 300 |
n = 200 |
n = 100 |
|||
|
|
|
|
|
|
|
|
|
60% |
0,0024 |
0,0016 |
0,0035 |
0,0026 |
0,0045 |
0,0051 |
|
50% |
0,0042 |
0,0024 |
0,0069 |
0,0039 |
0,0115 |
0,0072 |
|
40% |
0,0063 |
0,0039 |
0,0043 |
0,0061 |
0,0123 |
0,0111 |
|
30% |
0,0099 |
0,0057 |
0,0153 |
0,0088 |
0,0220 |
0,0186 |
|
20% |
0,0108 |
0,0107 |
0,0204 |
0,0144 |
0,0342 |
0,0292 |
|
10% |
0,0360 |
0,0229 |
0,0464 |
0,0339 |
0,0947 |
0,0636 |
|
5% |
0,0688 |
0,0464 |
0,1135 |
0,0731 |
0,1744 |
0,1370 |
Влияние аномальных измерений на оценки по цензурированным выборкам
Метод максимального правдоподобия наиболее хорошо адаптируется к форме регистрации наблюдений (группированные наблюдения, частично группированные, цензурированные), но это не означает, что в любой ситуации он оказывается наилучшим, так как ОМП в недостаточной мере обладают свойствами робастности. При увеличении степени цензурирования ОМП становятся более чувствительными к имеющимся в наблюдаемой части выборки отклонениям от предполагаемого закона распределения.
Исследование потерь информации, происходящих при
дополнительном группировании наблюдаемой области цензурированной справа
случайной величины, распределенной по экспоненциальному закону, показало, что
при большой степени цензурирования разбиение области наблюдения на интервалы
практически не сопровождается дополнительными потерями. То есть количества
информации Фишера в выборке, сильно цензурированной справа точкой ![]() , и в выборке, сгруппированной в 2 интервала с
разделяющей их границей
, и в выборке, сгруппированной в 2 интервала с
разделяющей их границей ![]() ,
отличаются незначительно. Это означает, что ОМП параметра экспоненциального
закона по сгруппированным в 2 интервала данным, получаемая в качестве решения
уравнения (3), в котором будет отсутствовать среднее слагаемое, и имеющая вид
[10]
,
отличаются незначительно. Это означает, что ОМП параметра экспоненциального
закона по сгруппированным в 2 интервала данным, получаемая в качестве решения
уравнения (3), в котором будет отсутствовать среднее слагаемое, и имеющая вид
[10]
![]() (6)
(6)
обладает практически той же асимптотической дисперсией, что и ОМП по цензурированной выборке, но является более робастной.
На получаемые оценки параметров существенное влияние оказывает наличие в выборке аномальных измерений. Многочисленные вычислительные эксперименты показали, что присутствие аномальных измерений в наблюдаемой области сильно цензурированной выборки отражается на оценках еще более заметно.
В качестве примера, для выборки, смоделированной по
распределению Вейбулла объемом 1000 наблюдений, вычислили ОМП параметров (![]() ,
, ![]() ).
Затем два правых наблюдения 2.4451 и 2.7853 были заменены на 12.4451 и
12.7853. ОМП, вычисленные по полной и цензурированным слева выборкам представлены
в левом столбце табл. 8 и, как видим, получаются очень плохими.
).
Затем два правых наблюдения 2.4451 и 2.7853 были заменены на 12.4451 и
12.7853. ОМП, вычисленные по полной и цензурированным слева выборкам представлены
в левом столбце табл. 8 и, как видим, получаются очень плохими.
Если выборку процензурировать и справа, то получаемые ОМП должны стать более робастными [11,12]. Выборки, цензурированные слева, дополнительно были процензурированы справа точкой 2.13, правее которой попало 10 наблюдений. Результаты вычислений по выборке, цензурированной с двух сторон (степень цензурирования слева менялась как и ранее), приведены во второй колонке этой же таблицы.
L-оценки (с использованием выборочных квантилей) и MD-оценки
обладают лучшими свойствами робастности по сравнению с ОМП [13]. MD-оценки
получаются при минимизации расстояния между эмпирической и теоретической
функциями распределения. В качестве меры близости эмпирического и теоретического
распределений можно использовать статистики непараметрических критериев
согласия. Особенностью получения MD-оценок по цензурированным данным
является неопределенность поведения эмпирической функции распределения на
интервалах цензурирования. Чтобы устранить эту неопределенность, необходимо
сделать предположения о характере согласия наблюдений и теоретической модели.
Так, например, если предположить, что в интервалах цензурирования эмпирическая
функция распределения проходит на наименьшем расстоянии от теоретической, то
мы получим оценку “крайнего оптимиста”, если же предположить обратное (на
максимально возможном расстоянии), то получим оценку “крайнего пессимиста”. В
последней колонке табл. 8 представлены MD-оценки параметров, полученные
минимизацией статистики, используемой в критерии ![]() -Мизеса, с точки зрения “крайнего оптимиста”.
-Мизеса, с точки зрения “крайнего оптимиста”.
Таблица 8.
Влияние аномальных наблюдений на точность оценивания параметров распределения Вейбулла по цензурированной слева выборке (n=1000)
|
Наблю- даемая |
ОМП по цензурированной слева выборке |
ОМП по выборке, цензурированной с двух сторон |
MD-оценки по цензурированной слева выборке |
|||
|
часть % |
|
|
|
|
|
|
|
100 |
1.5209 |
0.9895 |
2.0334 |
0.9799 |
1.9634 |
0.9813 |
|
60 |
1.4280 |
0.9539 |
1.9644 |
0.9821 |
1.9533 |
0.9805 |
|
50 |
1.3830 |
0.9314 |
1.9564 |
0.9807 |
1.9407 |
0.9794 |
|
40 |
1.3285 |
0.8979 |
1.9381 |
0.9771 |
1.9563 |
0.9814 |
|
30 |
1.2621 |
0.8579 |
1.9955 |
0.9902 |
2.0162 |
0.9896 |
|
20 |
1.1338 |
0.7606 |
1.8969 |
0.9634 |
1.8574 |
0.9566 |
|
10 |
0.9569 |
0.5903 |
1.9288 |
0.9723 |
1.9217 |
0.9709 |
|
5 |
0.7446 |
0.3754 |
1.8041 |
0.9264 |
1.7649 |
0.9175 |
Как видим, на робастные оценки и при сильно цензурированных выборках в меньшей степени отражается наличие аномальных измерений.
Цензурированные
выборки и оптимальное группирование
При исследованиях надежности не редкой оказывается ситуация, когда в наблюдаемой области сильно цензурированной выборки (например, справа) точные моменты выхода изделий из строя не могут фиксироваться. В этом случае проверка работоспособности осуществляется в конкретные заданные моменты времени. По существу вследствие условий регистрации наблюдений имеется возможность получить только полностью группированную выборку, по которой и приходится оценивать параметры распределения.
В связи с рассмотренной ситуацией нельзя не сделать следующего замечания. Совершенно непонятно, почему в п. 5.1.5 руководящего документа по стандартизации РД 50-690-89 [14] в такой ситуации рекомендуется использовать биномиальное распределение. Ничто не мешает определять параметры надежности, опираясь на тот закон распределения, модель которого является наиболее подходящей для конкретной ситуации. Например, для вычисления ОМП параметров достаточно численно решить систему вида (2), в которой в левой части будет только первое слагаемое.
Если проверка работоспособности может проводиться только в фиксированные
моменты времени, возникает естественный вопрос, как при заданной степени цензурирования
выбирать моменты регистрации так, чтобы потери информации о наблюдаемом
законе (о параметрах надежности) были минимальны. Можно решить задачу
асимптотически оптимального группирования (АОГ), при которой минимизируются
потери в количестве информации Фишера (минимизируется асимптотическая дисперсия
оценки параметра по группированным данным или асимптотическая обобщенная
дисперсия оценки вектора параметров) [2,12,15,16]. Однако в данном случае из-за
заданной степени цензурирования справа будем иметь задачу с дополнительным
ограничением вида ![]() (или
(или
![]() ):
):
![]() ,
(7)
,
(7)
![]() .
.
где информационная матрица Фишера по группированным данным
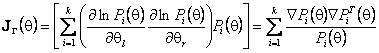 .
(8)
.
(8)
Для рассмотренных в данной работе распределений решения задачи АОГ может быть
получено в виде инвариантном относительно параметров распределений. Например, в
табл. 9 представлены решения задачи АОГ для масштабного параметра
экспоненциального распределения при заданной степени цензурировании справа,
где оптимальные квантили заданы в виде ![]() . Решение аналогичной задачи при цензурировании слева
приведено в табл. 10. В последнем случае дополнительное ограничение в задаче
(7) принимает вид:
. Решение аналогичной задачи при цензурировании слева
приведено в табл. 10. В последнем случае дополнительное ограничение в задаче
(7) принимает вид: ![]() (или
(или ![]() ).
В таблицах указано, какая часть информации сохраняется в цензурированной
выборке по отношению к полной, а также относительная информация
).
В таблицах указано, какая часть информации сохраняется в цензурированной
выборке по отношению к полной, а также относительная информация ![]() , характеризующая, какое количество информации
сохраняется при группировании наблюдаемой области. Эти же таблицы дают
решение задачи АОГ для масштабного параметра распределения Вейбулла при
, характеризующая, какое количество информации
сохраняется при группировании наблюдаемой области. Эти же таблицы дают
решение задачи АОГ для масштабного параметра распределения Вейбулла при 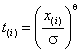 , а при
, а при 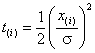 для
параметра распределения Рэлея. Отметим, что при той же степени цензурировании
слева в выборке сохраняется существенно больше информации о соответствующем
параметре распределения, чем при цензурировании справа.
для
параметра распределения Рэлея. Отметим, что при той же степени цензурировании
слева в выборке сохраняется существенно больше информации о соответствующем
параметре распределения, чем при цензурировании справа.
Таблица 9.
Асимптотически оптимальное группирование наблюдаемой области слева при цензурировании справа для параметров распределений экспоненциального, Рэлея и масштабного параметра Вейбулла
|
k |
|
|
|
|
|
|
|
|
A |
|
Доступны наблюдению 50% выборки: |
|||||||||
|
2 |
0,6931 |
|
|
|
|
|
|
|
0,9609 |
|
3 |
0,4339 |
0,6931 |
|
|
|
|
|
|
0,9874 |
|
4 |
0,1832 |
0,4087 |
0,6931 |
|
|
|
|
|
0,9954 |
|
5 |
0,1204 |
0,2708 |
0,4550 |
0,6931 |
|
|
|
|
0,9973 |
|
6 |
0,1124 |
0,2486 |
0,3534 |
0,4984 |
0,6931 |
|
|
|
0,9983 |
|
7 |
0,1003 |
0,2076 |
0,3123 |
0,4022 |
0,5208 |
0,6931 |
|
|
0,9988 |
|
8 |
0,0990 |
0,2175 |
0,3040 |
0,3859 |
0,4574 |
0,5726 |
0,6931 |
|
0,9991 |
|
9 |
0,0791 |
0,1571 |
0,2372 |
0,3094 |
0,3767 |
0,4706 |
0,5628 |
0,6931 |
0,9993 |
|
Доступны наблюдению 40%
выборки: |
|||||||||
|
2 |
0,5108 |
|
|
|
|
|
|
|
0,9785 |
|
3 |
0,1660 |
0,5108 |
|
|
|
|
|
|
0,9930 |
|
4 |
0,1744 |
0,3260 |
0,5108 |
|
|
|
|
|
0,9976 |
|
5 |
0,1392 |
0,2566 |
0,3498 |
0,5108 |
|
|
|
|
0,9985 |
|
6 |
0,0922 |
0,1832 |
0,2937 |
0,3750 |
0,5108 |
|
|
|
0,9991 |
|
7 |
0,0684 |
0,1497 |
0,2222 |
0,3026 |
0,3993 |
0,5108 |
|
|
0,9994 |
|
8 |
0,0810 |
0,1543 |
0,2286 |
0,2858 |
0,3376 |
0,4135 |
0,5108 |
|
0,9995 |
|
9 |
0,0547 |
0,1162 |
0,1911 |
0,2484 |
0,3063 |
0,3562 |
0,4207 |
0,5108 |
0,9996 |
|
Доступны наблюдению 30%
выборки: |
|||||||||
|
2 |
0,3567 |
|
|
|
|
|
|
|
0,9895 |
|
3 |
0,1035 |
0,3567 |
|
|
|
|
|
|
0,9961 |
|
4 |
0,1028 |
0,2000 |
0,3567 |
|
|
|
|
|
0,9987 |
|
5 |
0,1087 |
0,1979 |
0,2831 |
0,3567 |
|
|
|
|
0,9993 |
|
6 |
0,0685 |
0,1311 |
0,1843 |
0,2597 |
0,3567 |
|
|
|
0,9995 |
|
7 |
0,0530 |
0,1180 |
0,1900 |
0,2378 |
0,2821 |
0,3567 |
|
|
0,9997 |
|
8 |
0,0494 |
0,0994 |
0,1482 |
0,1914 |
0,2483 |
0,2891 |
0,3567 |
|
0,9998 |
|
9 |
0,0490 |
0,0923 |
0,1264 |
0,1649 |
0,2149 |
0,2449 |
0,2980 |
0,3567 |
0,9998 |
|
Доступны наблюдению 20%
выборки: |
|||||||||
|
2 |
0,2231 |
|
|
|
|
|
|
|
0,9959 |
|
3 |
0,0830 |
0,2231 |
|
|
|
|
|
|
0,9988 |
|
4 |
0,0608 |
0,1222 |
0,2231 |
|
|
|
|
|
0,9995 |
|
5 |
0,0656 |
0,1158 |
0,1552 |
0,2231 |
|
|
|
|
0,9997 |
|
6 |
0,0342 |
0,0704 |
0,1226 |
0,1646 |
0,2231 |
|
|
|
0,9998 |
|
7 |
0,0369 |
0,0762 |
0,1071 |
0,1344 |
0,1738 |
0,2231 |
|
|
0,9999 |
|
8 |
0,0311 |
0,0613 |
0,0943 |
0,1227 |
0,1463 |
0,1788 |
0,2231 |
|
0,9999 |
|
9 |
0,0279 |
0,0560 |
0,0841 |
0,1101 |
0,1332 |
0,1651 |
0,1856 |
0,2231 |
0,9999 |
|
Доступны наблюдению 10%
выборки: |
|||||||||
|
2 |
0,1054 |
|
|
|
|
|
|
|
0,9991 |
|
3 |
0,0396 |
0,1054 |
|
|
|
|
|
|
0,9997 |
|
4 |
0,0271 |
0,0579 |
0,1054 |
|
|
|
|
|
0,9999 |
|
5 |
0,0231 |
0,0503 |
0,0707 |
0,1054 |
|
|
|
|
0,9999 |
|
6 |
0,0241 |
0,0468 |
0,0652 |
0,0799 |
0,1054 |
|
|
|
1,0000 |
|
7 |
0,0180 |
0,0376 |
0,0523 |
0,0649 |
0,0824 |
0,1054 |
|
|
1,0000 |
|
8 |
0,0156 |
0,0304 |
0,0454 |
0,0584 |
0,0694 |
0,0843 |
0,1054 |
|
1,0000 |
|
9 |
0,0132 |
0,0266 |
0,0400 |
0,0523 |
0,0632 |
0,0779 |
0,0880 |
0,1054 |
1,0000 |
|
Доступны наблюдению 5% выборки: |
|||||||||
|
2 |
0,0513 |
|
|
|
|
|
|
|
0,9998 |
|
3 |
0,0280 |
0,0513 |
|
|
|
|
|
|
0,9999 |
|
4 |
0,0162 |
0,0290 |
0,0513 |
|
|
|
|
|
1,0000 |
|
5 |
0,0108 |
0,0244 |
0,0345 |
0,0513 |
|
|
|
|
1,0000 |
|
6 |
0,0118 |
0,0228 |
0,0317 |
0,0389 |
0,0513 |
|
|
|
1,0000 |
|
7 |
0,0085 |
0,0179 |
0,0252 |
0,0313 |
0,0399 |
0,0513 |
|
|
1,0000 |
|
8 |
0,0079 |
0,0154 |
0,0224 |
0,0286 |
0,0340 |
0,0411 |
0,0513 |
|
1,0000 |
|
9 |
0,0065 |
0,0129 |
0,0196 |
0,0256 |
0,0309 |
0,0379 |
0,0429 |
0,0513 |
1,0000 |
Таблица 10.
Асимптотически оптимальное группирование наблюдаемой области справа при цензурировании слева для параметров распределений экспоненциального, Рэлея и масштабного параметра Вейбулла
|
k |
|
|
|
|
|
|
|
|
A |
|
Доступны наблюдению
50% выборки: |
|||||||||
|
2 |
0,6931 |
|
|
|
|
|
|
|
0,4900 |
|
3 |
0,6931 |
2,2895 |
|
|
|
|
|
|
0,8203 |
|
4 |
0,6931 |
1,7722 |
3,5899 |
|
|
|
|
|
0,9069 |
|
5 |
0,6931 |
1,4681 |
2,4594 |
4,0684 |
|
|
|
|
0,9444 |
|
6 |
0,6931 |
1,3058 |
2,0665 |
3,0717 |
4,7206 |
|
|
|
0,9627 |
|
7 |
0,6931 |
1,1940 |
1,7910 |
2,5409 |
3,5576 |
5,1612 |
|
|
0,9733 |
|
8 |
0,6931 |
1,1359 |
1,6428 |
2,2527 |
2,9876 |
4,0477 |
5,6467 |
|
0,9799 |
|
9 |
0,6931 |
1,0754 |
1,5134 |
2,0258 |
2,6431 |
3,4202 |
4,4732 |
6,1480 |
0,9843 |
|
Доступны наблюдению
40% выборки: |
|||||||||
|
2 |
0,9163 |
|
|
|
|
|
|
|
0,5832 |
|
3 |
0,9163 |
2,5108 |
|
|
|
|
|
|
0,8531 |
|
4 |
0,9163 |
2,0482 |
3,1974 |
|
|
|
|
|
0,9241 |
|
5 |
0,9163 |
1,7287 |
2,8724 |
4,4903 |
|
|
|
|
0,9540 |
|
6 |
0,9163 |
1,5346 |
2,3122 |
3,3683 |
4,9807 |
|
|
|
0,9695 |
|
7 |
0,9163 |
1,4490 |
2,0621 |
2,8736 |
3,9904 |
5,9297 |
|
|
0,9777 |
|
8 |
0,9163 |
1,3647 |
1,8877 |
2,5157 |
3,2907 |
4,3388 |
6,0731 |
|
0,9835 |
|
9 |
0,9163 |
1,2973 |
1,7333 |
2,2419 |
2,8531 |
3,6201 |
4,6549 |
6,2863 |
0.9872 |
|
Доступны наблюдению
30% выборки: |
|||||||||
|
2 |
1,2040 |
|
|
|
|
|
|
|
0,6744 |
|
3 |
1,2040 |
2,8102 |
|
|
|
|
|
|
0,8852 |
|
4 |
1,2040 |
2,2122 |
3,8074 |
|
|
|
|
|
0,9415 |
|
5 |
1,2040 |
1,9801 |
3,0371 |
4,6433 |
|
|
|
|
0,9645 |
|
6 |
1,2040 |
1,8586 |
2,7050 |
3,8781 |
5,7241 |
|
|
|
0,9755 |
|
7 |
1,2040 |
1,7351 |
2,3713 |
3,2031 |
4,2953 |
6,0054 |
|
|
0,9827 |
|
8 |
1,2040 |
1,6348 |
2,1406 |
2,7479 |
3,4973 |
4,5119 |
6,0949 |
|
0,9872 |
|
9 |
1,2040 |
1,5884 |
2,0288 |
2,5438 |
3,1628 |
3,9388 |
4,9825 |
6,6065 |
0,9900 |
|
Доступны наблюдению
20% выборки: |
|||||||||
|
2 |
1,6094 |
|
|
|
|
|
|
|
0,7640 |
|
3 |
1,6094 |
3,2052 |
|
|
|
|
|
|
0,9168 |
|
4 |
1,6094 |
2,5527 |
4,0551 |
|
|
|
|
|
0,9573 |
|
5 |
1,6094 |
2,3702 |
3,3916 |
4,9465 |
|
|
|
|
0,9743 |
|
6 |
1,6094 |
2,2474 |
3,0740 |
4,1902 |
5,9068 |
|
|
|
0,9825 |
|
7 |
1,6094 |
2,1365 |
2,7799 |
3,5935 |
4,6947 |
6,2622 |
|
|
0,9875 |
|
8 |
1,6094 |
2,0453 |
2,5554 |
3,1697 |
3,9425 |
4,9869 |
6,6489 |
|
0,9907 |
|
9 |
1,6094 |
1,9946 |
2,4359 |
2,9507 |
3,5661 |
4,3295 |
5,3401 |
6,9269 |
0,9927 |
|
Доступны наблюдению
10% выборки: |
|||||||||
|
2 |
2,3026 |
|
|
|
|
|
|
|
0,8549 |
|
3 |
2,3026 |
3,9030 |
|
|
|
|
|
|
0,9489 |
|
4 |
2,3026 |
3,4216 |
5,2016 |
|
|
|
|
|
0,9736 |
|
5 |
2,3026 |
3,0606 |
4,1061 |
5,7826 |
|
|
|
|
0,9842 |
|
6 |
2,3026 |
2,9362 |
3,7419 |
4,8317 |
6,5212 |
|
|
|
0,9893 |
|
7 |
2,3026 |
2,8268 |
3,4606 |
4,2576 |
5,3345 |
7,0163 |
|
|
0,9923 |
|
8 |
2,3026 |
2,7403 |
3,2527 |
3,8684 |
4,6373 |
5,6656 |
7,2511 |
|
0,9943 |
|
9 |
2,3026 |
2,6756 |
3,1019 |
3,5995 |
4,1983 |
4,9508 |
5,9689 |
7,5623 |
0,9955 |
|
Доступны наблюдению
5% выборки: |
|||||||||
|
2 |
2,9957 |
|
|
|
|
|
|
|
0,9043 |
|
3 |
2,9957 |
4,7649 |
|
|
|
|
|
|
0,9658 |
|
4 |
2,9957 |
4,0105 |
5,6138 |
|
|
|
|
|
0,9828 |
|
5 |
2,9957 |
3,8010 |
4,8728 |
6,5195 |
|
|
|
|
0,9895 |
|
6 |
2,9957 |
3,6452 |
4,4619 |
5,5364 |
7,1709 |
|
|
|
0,9929 |
|
7 |
2,9957 |
3,4975 |
4,1010 |
4,8599 |
5,8867 |
7,5010 |
|
|
0,9950 |
|
8 |
2,9957 |
3,4223 |
3,9204 |
4,5201 |
5,2754 |
6,2944 |
7,8971 |
|
0,9962 |
|
9 |
2,9957 |
3,3695 |
3,7966 |
4,2949 |
4,8931 |
5,6436 |
6,6566 |
8,2499 |
0,9971 |
В ходе исследований были получены решения задачи АОГ наблюдаемой области (левой части при цензурировании справа и правой части при цензурировании слева) для ряда законов распределения. Анализ полученных таблиц АОГ позволяет отметить, что с ростом степени цензурирования наблюдаемые значения случайной величины несут всё меньшую часть информации, из сохранившейся в цензурированной выборке, и всё большая её часть содержится в квантили, определяющей область цензурирования (в количестве наблюдений в этой области). Этим, в частности, определяется достаточно высокая точность оценивания параметра экспоненциального закона с использованием этой единственной квантили.
Применение АОГ в ситуации, когда моменты отказов
фиксироваться не могут, позволяет получать ОМП параметров по группированным
данным, практически не уступающие по асимптотическим свойствам оценкам по
цензурированным. Конечно, для того, чтобы использовать решение задачи АОГ надо
знать значения параметров, которые-то как раз и требуется оценить. В этом
случае возможен следующий выход. В задачах контроля качества или испытаниях
надежности область значений параметров обычно бывает известна по результатам
предыдущих экспериментов. Тогда можно воспользоваться этой информацией для
выбора ![]() по прогнозируемым значениям
по прогнозируемым значениям ![]() . При не слишком больших ошибках прогноза выигрыш все
равно будет ощутим [10].
. При не слишком больших ошибках прогноза выигрыш все
равно будет ощутим [10].
Заключение
Подводя итог всему вышесказанному, зафиксируем основные факты.
В аналитически простом виде выражения для оценок параметров по цензурированным выборкам получаются лишь в некоторых частных случаях. Более перспективно определение оценок численными методами, для чего, вообще говоря, нет принципиальных трудностей.
При условии, что соответствующая параметрическая модель хорошо описывает закон распределения наблюдаемой случайной величины, можно достаточно точно оценивать параметры закона даже при очень сильно цензурированных выборках.
Идентифицировать параметрическую модель по малой выборке чрезвычайно сложно, так как можно указать (подобрать) множество моделей, одинаково хорошо описывающих выборочные данные с позиций различных критериев согласия. Особенности генеральной совокупности более четко проявляются с ростом объема выборки. Поэтому очевидно, что при больших объемах выборки можно достаточно точно находить оценки при большей степени цензурирования. Для иллюстрации этого на рис. 7 приведены результаты оценивания параметров распределения Вейбулла по цензурированной слева выборке объемом в 50 наблюдений, в которой были доступны наблюдению 20 последних значений. На рисунке отражены результаты проверки согласия полученного закона с полной выборкой. В данном случае мы видим существенное различие эмпирической и теоретической функций распределения в ненаблюдаемой части (при значениях ординат от 0 до 0.6). А на рис. 8 для выборки объемом в 200 наблюдений и большей степени цензурирования (наблюдалось 40 правых значений) получены уже очень хорошие оценки параметров, о чем говорят результаты проверки согласия найденного закона с полной выборкой.
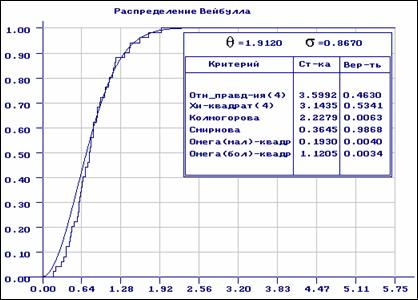
Рис. 7. Результаты проверки согласия полной выборки объемом 50
наблюдений с распределением Вейбулла, параметры которого определялись
по цензурированной слева выборке и степенью цензурирования 60%
(наблюдалось 20 правых выборочных значений из 50)
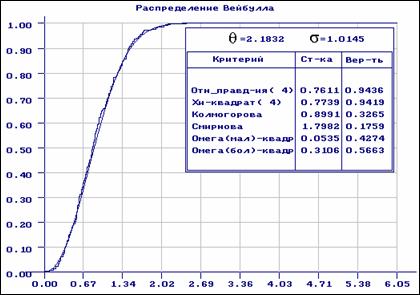
Рис. 8. Результаты проверки согласия полной выборки объемом 200
наблюдений с распределением Вейбулла, параметры которого определялись
по цензурированной слева выборке и степенью цензурирования 80%
(наблюдалось 40 правых выборочных значений из 200)
Цензурирование справа и слева для несимметричных законов может быть связано с различными потерями в количестве информации Фишера. Чем больше потери, тем больше асимптотическая дисперсия вычисляемых оценок. Величина потерь адекватно отражается на точности оценивания параметров.
При сильном цензурировании мы оцениваем параметры закона по левому или правому “хвосту” эмпирической функции распределения. И в этом случае на оценках в большей степени могут сказываться имеющиеся в выборке случайные отклонения от предполагаемого закона. Особенно резко это будет проявляться при малых объемах выборок. Поэтому естественно, что более предпочтительным является использование робастных оценок, в том числе ОМП по группированным наблюдениям, L-оценок и MD-оценок.
При проверке сложных гипотез следует помнить о том, что непараметрические критерии теряют свойство “свободы от распределения” [17]. В приводимых примерах (рис. 7-8), проверяя гипотезу о согласии закона, полученного по сильно цензурированной выборке, с полной выборкой (с той же самой, которую цензурировали), мы предполагали, что есть основание рассматривать проверяемые гипотезы как простые. Ситуация близка к той, когда по одной половине выборки оценивают параметры, а по другой - проверяют гипотезу о согласии. По крайней мере, ошибки не должны быть велики.
В данной работе мы не касались вопросов проверки гипотез о согласии по сильно
неполным выборкам. Нет принципиальных проблем в использовании критериев типа ![]() Пирсона, хотя большое количество наблюдений,
попавших в крайний интервал (интервалы), отразится на распределении статистики
[18]. Но проблемы есть в применении непараметрических критериев типа
Колмогорова, Смирнова и
Пирсона, хотя большое количество наблюдений,
попавших в крайний интервал (интервалы), отразится на распределении статистики
[18]. Но проблемы есть в применении непараметрических критериев типа
Колмогорова, Смирнова и ![]() Мизеса.
В случае простых гипотез можно воспользоваться подходом, связанным с
определением оценок сверху и снизу для статистик используемых критериев и рассматриваемым
нами в [19-21]. В случае сложных - вопрос остается открытым. Однако
стремительный прогресс компьютерной техники позволяет распространить этот
подход и на сложные гипотезы, используя аналогично [22] для идентификации
законов распределения статистик (их оценок сверху и снизу) методы
статистического моделирования, причем непосредственно в процессе проверки
гипотез по конкретной выборке.
Мизеса.
В случае простых гипотез можно воспользоваться подходом, связанным с
определением оценок сверху и снизу для статистик используемых критериев и рассматриваемым
нами в [19-21]. В случае сложных - вопрос остается открытым. Однако
стремительный прогресс компьютерной техники позволяет распространить этот
подход и на сложные гипотезы, используя аналогично [22] для идентификации
законов распределения статистик (их оценок сверху и снизу) методы
статистического моделирования, причем непосредственно в процессе проверки
гипотез по конкретной выборке.
ЛИТЕРАТУРА
1. Тихов М.С. Оценивание показателей качества по неполным выборкам // Надежность и контроль качества. 1996. № 11. С.16-24.
2. Куллдорф Г. Введение в теорию оценивания по группированным и частично группированным выборкам. - М.: Наука, 1966. - 176 с.
3. Кудлаев Э.М. Об оценивании параметров распределения по отрезкам вариационного ряда // Теория вероятностей и её применения. 1973. Т.18. № 3. С.655-662.
4. Агзамов С.К., Огульник Ю.М. Определение интервальных оценок и точности показателей долговечности по многократно усеченным выборкам // Надежность и контроль качества, 1976. № 9. С.49-54.
5. Баталова З.Г., Благовещенский Ю.Н. О точности оценок ресурсов элементов конструкций методом максимума правдоподобия при случайном усечении длительности наблюдений // Надежность и контроль качества, 1979. № 9. С.12-20.
6. Благовещенский Ю.Н. Анализ оценки максимального правдоподобия по случайно цензурированной выборке с малой долей отказов на примере экспоненциального распределения // Заводская лаборатория. 1982. Т. 48. № 3. С.50-52.
7. Скрипник В.М., Назин А.Е. Оценка надежности технических систем по цензурированным выборкам. – Минск: Наука и техника, 1981. – 144 с.
8. Скрипник В.М., Назин А.Е., Приходько Ю.Г. Анализ надежности технических систем по цензурированным выборкам. – М.: Радио и связь, 1988. – 183 с.
9. Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. - Новосибирск: Изд-во НГТУ, 1995. - 125 с.
10. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. - Новосибирск: Изд-во НГТУ, 1993. - 346 с.
11. Лемешко Б.Ю. Робастные методы оценивания и отбраковка аномальных измерений // Заводская лаборатория. 1997. Т.63. № 5. С.43-49.
12. Лемешко Б.Ю. Группирование наблюдений как способ получения робастных оценок // Надежность и контроль качества. 1997. № 5. С.26-35.
13. Шуленин В.П. Введение в робастную статистику. - Томск: Изд-во Том. ун-та, 1993. - 227 с.
14. РД 50-690-89. Надежность в технике. Методы оценки показателей надежности по экспериментальным данным. - М.: Изд-во стандартов, 1990.
15. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия // Заводская лаборатория, 1998. Т. 64. №1. С.56-64.
16. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений - это обеспечение максимальной мощности критериев // Надежность и контроль качества. 1997. № 8. С.3-14.
17. Орлов А.И. Распространенная ошибка при использовании критериев Колмогорова и омега-квадрат // Заводская лаборатория. 1985. Т. 51. № 1. С.60-62.
18.
Лемешко Б.Ю., Постовалов С.Н. О
зависимости предельных распределений статистик ![]() Пирсона и отношения правдоподобия от способа
группирования данных // Заводская лаборатория. 1998. Т. 64. № 5. С.56-63.
Пирсона и отношения правдоподобия от способа
группирования данных // Заводская лаборатория. 1998. Т. 64. № 5. С.56-63.
19. Лемешко Б.Ю., Постовалов С.Н. Статистический анализ одномерных наблюдений по частично группированным данным // Изв. вузов. Физика. - Томск, 1995. № 9. С.39-45.
20. Лемешко Б.Ю., Постовалов С.Н. Статистический анализ наблюдений, имеющих интервальное представление // Сб. научных трудов НГТУ. - Новосибирск: Изд-во НГТУ, 1996. № 1. С.3-12.
21. Лемешко Б.Ю., Постовалов С.Н. О решении задач статистического анализа интервальных наблюдений // Вычислительные технологии. 1997. Т.2. № 1. С.28-36.
22. Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов // Заводская лаборатория. 1998. Т. 64. № 3. С.61-72.