Критерии
Бартлетта, Кохрена и F-критерий при вероятностных законах, отличающихся от
нормального
Приложение 23. Верхние процентные (1%) точки для статистики Кохрена (нормальный закон, λ=2)
Приложение 24. Верхние процентные (5%) точки для статистики Кохрена (нормальный закон, λ=2)
Приложение 25. Процентные точки F-распределения (5%)
[Выход]
Ссылка:
Лемешко Б.Ю., Миркин Е.П. Критерии Бартлетта и Кокрена в измерительных задачах при вероятностных законах, отличающихся от нормального // Измерительная техника. 2004. № 10. – С. 10-16.
Дальнейшие результаты по критериям однородности дисперсий (критерий Фишера, критерий Бартлетта, критерий Кокрена, критерий Хартли, критерий Левене, мощность критерия):
Лемешко Б.Ю., Лемешко С.Б., Горбунова А.А. О применении и мощности критериев проверки однородности дисперсий. Ч. I. Параметрические критерии // Измерительная техника. 2010. № 3. – С.10-16.
Дальнейшие результаты по критериям однородности дисперсий (непараметрический критерий Ансари-Бредли, критерий Муда, критерий Сижела-Тьюки, критерий Кейпена, критерий Клотца, мощность критерия):
Лемешко Б.Ю., Лемешко С.Б., Горбунова А.А. О применении и мощности критериев проверки однородности дисперсий. Ч. II. Непараметрические критерии // Измерительная техника. 2010. № 5. – С.11-18.
См. также: Прикладная математическая статистика (материалы к семинарам)
Введение
[Вперед]
При статистическом контроле качества для проверки наличия возмущения в ходе процесса, как правило, используется ряд статистических критериев, с помощью которых проверяются гипотезы о постоянстве дисперсий контролируемого показателя или о равенстве этого показателя номинальному значению. Аналогичные задачи проверки гипотез возникают при поверке и аттестации средств измерений и испытательных лабораторий. В литературных источниках [1, 2] и стандартах [3] в этих целях рассматривается применение критериев Бартлетта [4], Кохрена [5] и F–критерия. Первые два критерия применяются для проверки гипотез о равенстве дисперсий совокупности выборок, а F–критерий – о равенстве математических ожиданий. В [3] применение критерия Кохрена предусматривается для выделения выбросов при анализе точности (прецизионности) измерений испытательных лабораторий.
Проверяемая
гипотеза о постоянстве дисперсии 
выборок
имеет вид:
.
(1)
а конкурирующая с ней гипотеза –
,
(2)
где неравенство выполняется, по
крайней мере, для одной пары индексов 
, 
.
Например, в
задаче контроля некоторого показателя гипотеза 
может утверждать, что, по
крайней мере, для двух моментов взятия выборок из общего числа моментов времени
m (m выборок,
взятых в разные моменты времени) дисперсия имеет разные значения.
Проверяемая гипотеза о постоянстве математических ожиданий задается в виде:
,
(3)
а конкурирующая –
,
(4)
по крайней мере, для одной пары
индексов , .
В качестве основного предположения при построении критериев Бартлетта, Кохрена и F–критерия и выводе предельных распределений статистик этих критериев выдвигалась принадлежность наблюдаемых случайных величин (ошибок измерений) нормальному закону распределения.
Известно, что ошибки измерительных приборов далеко не всегда описываются нормальным законом распределения [6]. Очевидно и то, что в задачах контроля качества регистрируемые отклонения контролируемого показателя технологического процесса от номинального (заданного) значения при условии стационарности процесса не всегда подчиняются нормальному закону. При этом сам процесс может удовлетворять всем выдвигаемым требованиям, например, по качеству продукции.
Как поведут себя рассматриваемые критерии при нарушении предположений о нормальности наблюдаемых величин? Возможно ли в изменившейся ситуации применение данных критериев в их классическом виде или такие действия приведут к некорректности результатов?
Цель данной работы состояла в исследовании распределений статистик трех вышеупомянутых критериев при различной степени отклонения распределения наблюдаемых случайных величин от нормального закона и в выработке рекомендаций по применению данных критериев в таких условиях. Представленные результаты дополняют исследования [7] о поведении статистик критериев, используемых для проверки гипотез о дисперсиях и математических ожиданиях. Как и в [7], основе данных исследований лежала развиваемая методика статистического моделирования и компьютерного анализа, хорошо зарекомендовавшая себя при исследовании статистических закономерностей в [8, 9].
Критерий
Бартлетта
[Вперед][Назад]
Статистика критерия Бартлетта вычисляется в соответствии с соотношением [2]:
где 
– объемы выборок, 
, если математическое ожидание
известно, и 
,
если неизвестно, 
,
,
– оценки выборочных
дисперсий. При неизвестном математическом ожидании оценки 
, где 
и . Если гипотеза 
верна, все 
и выборки извлекаются из
нормальной генеральной совокупности, то статистика (5) приближенно
подчиняется 
-распределению.
При нормально
распределенных наблюдаемых (измеряемых) величинах распределение статистики (5) практически не зависит от изменения объема выборки. Например,
на рис. 1 приведены практически совпадающие функции
распределения статистики критерия Бартлетта (5) при
различных объемах выборок (
).
Это означает, что в случае нормальности наблюдаемых величин выводы остаются
корректными и при очень малых объемах анализируемых выборок.
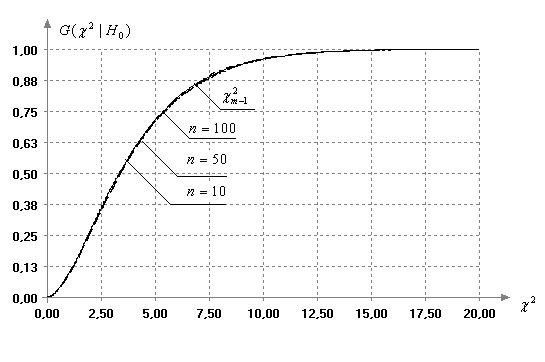
Рис.
1. Функции распределения статистики классического критерия Бартлетта при
различных объемах выборок при 
В то же время, распределения статистики (5) очень чувствительны к отклонениям наблюдаемого закона от нормального. Вид распределения статистики (5) исследовался при различных наблюдаемых законах, в частности, в случае принадлежности моделируемых выборок законам логистическому с плотностью
,
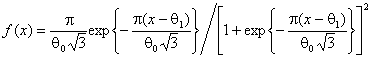Лапласа с плотностью
,
экспоненциальному семейству распределений с различными параметрами формы с плотностью
,
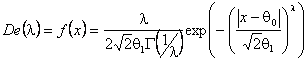(6)
где l – параметр формы. Законы нормальный и Лапласа являются частными случаями данного семейства распределений при значениях параметра формы 2 и 1 соответственно. Семейство (6) может быть хорошей моделью для законов распределения ошибок различных измерительных систем.
Рис.
2 отражает зависимость распределений статистики (5) от вида
наблюдаемого закона при различных объемах выборок.
Видно, что при отклонении закона распределения наблюдаемого показателя от
нормального закона распределение статистики критерия Бартлетта (5)
существенно отличается от -распределения.
При этом распределения статистики становятся более зависимыми от объема
выборки, чем в случае нормального закона.
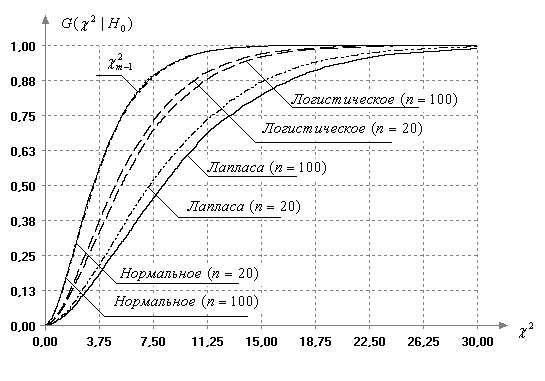
Рис. 2. Функции
распределения статистики Бартлетта при отклонении закона распределения
наблюдаемого показателя от нормального при различных объемах выборки и
Следовательно,
если опираться на классическое предельное -распределение
в случае принадлежности наблюдаемой величины распределению Лапласа или
логистическому, то даже при справедливости проверяемой гипотезы о равенстве дисперсий она
с большой вероятностью будет отклоняться. На рис. 3
показано, как меняется распределение статистики Бартлетта, если наблюдаемая
случайная величина подчиняется экспоненциальному семейству распределений с
различными значениями параметра формы. Вид функций распределения статистики
Бартлетта на рис. 3 показывает, что в случаях, когда
наблюдаемая случайная величина принадлежит распределению экспоненциального
семейства, более плосковершинному по сравнению с нормальным, то, если мы
воспользуемся классическим предельным распределением, неверная проверяемая
гипотеза может
приниматься с большой вероятностью.
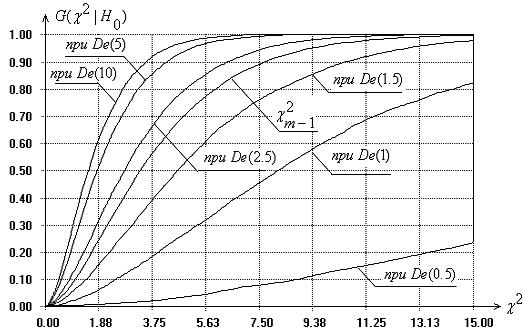
Рис. 3. Функции
распределения статистики критерия Бартлетта в случае распределений
экспоненциального семейства 
с
различными значениями параметра формы при 
и
Представленная на рис. 3 картина
хорошо иллюстрирует рассуждения [10], изложенные в [11], по поводу применения классического критерия Бартлетта [4] в случае нарушения предположений о нормальности. При законах
распределения наблюдаемых величин, более плосковершинных по сравнению с
нормальным (с отрицательными значениями коэффициента эксцесса 
, где 
– четвертый центральный момент, 
– дисперсия закона)
классический критерий Бартлетта [4] затушевывает разницу в
дисперсиях, а в случае более островершинных (при 
) – находит различие в
дисперсиях, когда такого различия нет. Подчеркнем, что ниже аналогичную
картину для критерия Кохрена отражает рис. 6.
При законах
распределения наблюдений, отличающихся от нормального, распределения
статистики Бартлетта существенно зависят от объема выборки 
, однако достаточно хорошо
сходятся к некоторым предельным законам.
В случае
принадлежности наблюдаемых величин распределениям экспоненциального семейства
на основании результатов статистического моделирования нами построены таблицы
верхних процентных точек (1%, 5%, 10%) статистики Бартлетта для значений параметра
формы 
=0.5, 1, 1.5, 3, 4, 5, 10 при
различных m и значений n=10, 50, 100. Процентные точки строились по смоделированным
эмпирическим распределениям статистик объемом в 50000 и усреднением по ряду
экспериментов. Полученные процентные точки представлены в таблицах приложений 1-7
Критерий Кохрена
[Вперед][Назад]
В том случае,
когда все одинаковы,
, возможно
использование более простого критерия Кохрена. Статистика Q критерия
Кохрена выражается формулой [2]
где 
,
где m –
число независимых оценок дисперсий (число выборок). В [2]
говорится, что критерий Кохрена несколько уступает по мощности критерию Бартлетта.
Распределения статистики Кохрена сильно зависят от объема наблюдаемых выборок. Поэтому в справочной литературе приводятся только таблицы процентных точек [2], которые и используются при проверке гипотез. На рис. 4 приведены полученные в результате компьютерного моделирования функции распределения статистики (7) при различных объемах выборок. В данном случае число оценок дисперсий m=5.
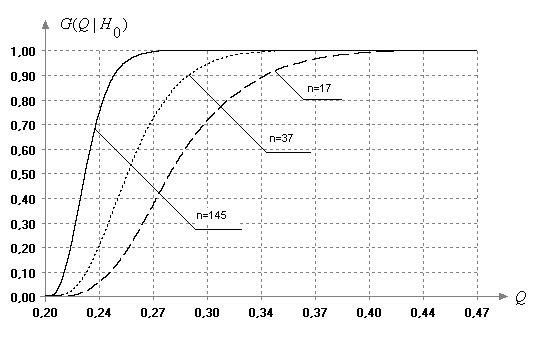
Рис. 4. Функции распределения статистики критерия Кохрена при различных объемах выборок при m=5
Как и критерий
Бартлетта, критерий Кохрена используется в предположении, что наблюдаемая
случайная величина принадлежит нормальному закону. Поэтому, представляет
интерес, насколько сильно меняется распределение статистики Кохрена (7) в случае определенных отклонений закона распределения
наблюдаемой случайной величины (контролируемого показателя) от нормального. На
рис. 5 представлен вид функции распределения статистики (7), когда при справедливости проверяемой гипотезы 
о равенстве дисперсий
выборки наблюдений принадлежат различным законам: нормальному, логистическому
и Лапласа. Различие в законах распределения статистики (7)
сохраняет характер при различных объемах выборок. На рис. 6
показано, как существенно меняется распределение статистики Кохрена, если
наблюдаемая случайная величина подчиняется распределениям экспоненциального
семейства с различными параметрами формы. Вид распределений статистики (7), представленных на рисунках 5 и 6, позволяет утверждать, что при нарушении нормальности
выборок, если этого не учитывать, проверяемая гипотеза о равенстве дисперсий
может с большой вероятностью отвергаться в случае ее справедливости и приниматься
в случае несправедливости.
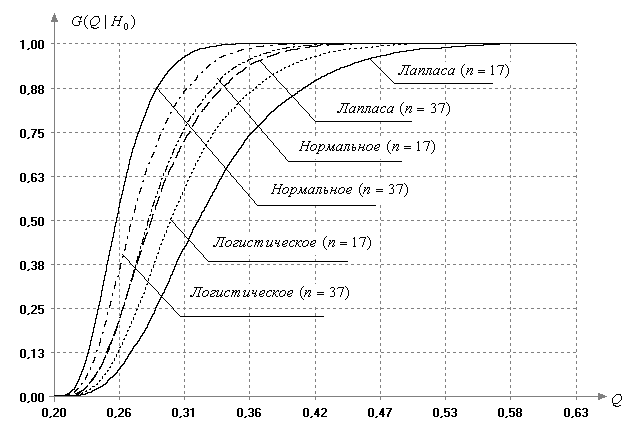
Рис. 5. Функции распределения статистики критерия Кохрена при отклонении закона распределения наблюдаемого показателя от нормального при различных объемах выборки при m=5
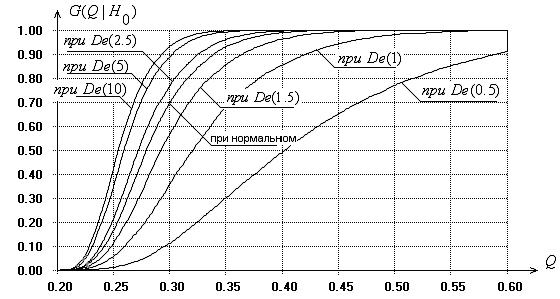
Рис. 6. Функции
распределения статистики критерия Кохрена в случае распределений
экспоненциального семейства с различными значениями параметра формы при 
и
Распределения статистики Кохрена сильно зависят от объема выборок и очень зависят от вида наблюдаемого закона. К тому же в [2] утверждается, что по мощности критерий Кохрена уступает критерию Бартлетта. Казалось бы, все это делает его мало привлекательным при произвольных наблюдаемых законах.
Однако на самом деле, как показали наши исследования, в случае принадлежности наблюдений нормальному закону критерий Кохрена превосходит по мощности критерий Бартлетта.
Например, в таблице 1 для сравнения приведены значения мощности 
критериев относительно
трех различных альтернатив при различных объемах выборок для вероятностей ошибок
первого рода 
=0.1,
0.05, 0.01. Конкурирующая гипотеза предполагает, что одна из выборок, например,
выборка с номером имеет
некоторую другую дисперсию. Рассмотрены альтернативы 
: 
; 
: 
и 
: 
. Остальные 
выборки принадлежат
нормальному закону с 
(
). Значения мощности приведены
для числа выборок и
достаточно больших объемов выборок, т.к. при малых мощность данных критериев,
то есть их способность различать близкие альтернативы, очень мала.
Таблица 1. Мощность
критериев Бартлетта и Кохрена относительно альтернатив ,,
|
|
|
|
|||||
|
|
|
|
|||||
|
Критерий Бартлетта |
Критерий Кохрена |
Критерий Бартлетта |
Критерий Кохрена |
Критерий Бартлетта |
Критерий Кохрена |
||
|
200 |
0.1 |
0.1706 |
0.2342 |
0.3600 |
0.4778 |
0.8346 |
0.9196 |
|
0.05 |
0.1030 |
0.1078 |
0.2534 |
0.3022 |
0.7568 |
0.8370 |
|
|
0.01 |
0.0274 |
0.0306 |
0.1064 |
0.1362 |
0.5558 |
0.6708 |
|
|
500 |
0.1 |
0.2608 |
0.3488 |
0.6712 |
0.7976 |
0.9968 |
0.9990 |
|
0.05 |
0.1682 |
0.1938 |
0.5554 |
0.6598 |
0.9926 |
0.9974 |
|
|
0.01 |
0.0608 |
0.0726 |
0.3330 |
0.4288 |
0.9702 |
0.9860 |
|
|
1000 |
0.1 |
0.4556 |
0.4990 |
0.9432 |
0.9686 |
0.9998 |
1 |
|
0.05 |
0.3340 |
0.3816 |
0.8998 |
0.9410 |
0.9998 |
1 |
|
|
0.01 |
0.1368 |
0.2034 |
0.7422 |
0.8560 |
0.9996 |
1 |
|
Стандарт [3] предполагает применение критерия Кохрена при малых объемах
выборок: 
. Поэтому
необходимо иметь ввиду, что в такой ситуации можно надежно различать лишь
достаточно далекие альтернативы, когда дисперсии отличаются “в разы”.
В случае
принадлежности наблюдаемых величин распределениям экспоненциального семейства
на основании результатов статистического моделирования нами построены таблицы
верхних процентных точек (1%, 5%, 10%) статистики Кохрена для значений
параметра формы =0.5, 1, 3, 5, 10 при
различных m и ряда значений n. Процентные точки строились по смоделированным
эмпирическим распределениям статистик объемом в 50000 и усреднением по ряду
экспериментов. Полученные процентные точки представлены в таблицах приложений
8-22.
F-критерий
[Вперед][Назад]
В литературных источниках [1] утверждается, что если гипотеза о постоянстве дисперсий верна (это можно проверить с помощью критериев Бартлетта или Кохрена), то с помощью F-критерия можно проверить гипотезу о постоянстве математического ожидания. В этом случае проверяемая и конкурирующая гипотезы имеют вид (3) – (4).
Пусть у нас
имеется выборок
объема . Общая сумма
квадратов отклонений по всем выборкам
,
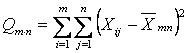где
,
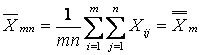раскладывается на два компонента
,
,
.
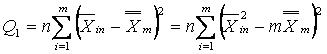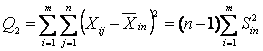Компонент 
является мерой различия в
уровнях настройки между 
выборками,
в то время как 
определяет
различие в уровнях настройки внутри выборок.
Для проверки гипотезы (3) можно воспользоваться F-критерием, основанным на статистике:
.
(8)
Если все
выборки извлекаются из нормальной генеральной совокупности, то при
справедливости гипотезы статистка
(8) имеет распределение Фишера со степенями свободы 
= m-1 в числителе и 
= m(n-1) в знаменателе [1].
Исследования методами
статистического моделирования распределений статистики (8)
при различных объемах выборок показали, что статистика (8) F-критерия уже при достаточно
малых объемах выборок (но достаточно больших 
) практически не зависит от величины
. Эмпирические
функции распределения статистики для различных объемов выборок при нормальном
распределении контролируемого показателя приведены на рис. 7.
Вид 
–распределений
Фишера при больших также
практически не меняется.
F-критерий, как и
критерии проверки гипотез о дисперсиях, предполагает, что наблюдаемая величина
имеет нормальное распределение. Именно в этом случае предельным распределением
статистики (8) является 
–распределение
Фишера. Как ведет себя функция распределения статистики (8)
при нарушении предположения о нормальности иллюстрирует рис. 8,
на котором представлены функции распределения статистики (8)
при наблюдаемых законах нормальном, логистическом, логнормальном и Лапласа при
различных объемах выборок. Визуально при одном и том же объеме выборок
полученные распределения практически не отличаются. Применение критериев
согласия также позволяет утверждать, что значимого изменения распределений
статистик из-за нарушений предположений о нормальности не происходит. То есть F-критерий оказывается
очень устойчивым, и его применение с опорой на предельное –распределение Фишера остается
корректным и в тех случаях, когда наблюдаемый закон существенно отличается от
нормального.
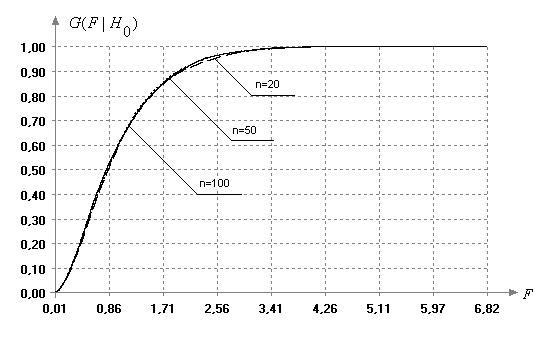
Рис.
7. Функции распределения статистики F-критерия при различных объемах выборок при
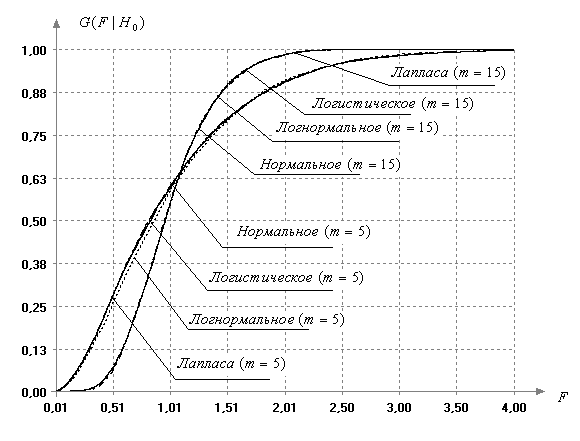
Рис.
8. Функции распределения статистики F-критерия при различных наблюдаемых законах и различных m ()
Заключение
[Вперед][Назад]
Таким образом,
критерии Бартлетта и Кохрена весьма чувствительны к отклонениям закона
наблюдаемого показателя от нормального. Корректное применение этих критериев
требует знания распределений статистик при конкретных законах наблюдаемых
величин. Если наблюдаемый закон отличается от нормального, применение
классических результатов недопустимо. В тех случаях, когда наблюдаемые величины
хорошо описываются распределением экспоненциального семейства с некоторым
параметром формы ,
можно воспользоваться полученными в данной работе таблицами соответствующих
верхних процентных точек.
При необходимости регулярных проверок гипотез о дисперсиях при некоторой конкретной модели наблюдаемого закона для нахождения (в этих условиях) распределения статистики критерия Бартлетта (или Кохрена) можно рекомендовать воспользоваться методикой статистического моделирования и последующего компьютерного анализа полученной закономерности.
В отличие от
критериев Бартлетта и Кохрена F-критерий намного устойчивее к отклонениям от нормальности
контролируемого показателя. Применяя F-критерий, классическим предельным 
–распределением Фишера можно
пользоваться при существенных отклонениях наблюдаемого закона от нормального.
Работа выполнена при финансовой поддержке Минобразования РФ (проект № Т02-3.3-3356)
[Назад][В
начало]
1. Миттаг Х.-Й., Ринне Х. Статистические методы обеспечения качества. – М.: Машиностроение. 1995. – 600 с.
2. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. - 416 с.
3. ГОСТ Р ИСО 5725–1–2002 ÷ ГОСТ Р ИСО 5725–6–2002. Точность (правильность и прецизионность) методов и результатов измерений. – М.: Изд-во стандартов. 2002.
4. Bartlett M.S. Properties
of sufficiency of statistical tests // Proc. Roy. Soc., 1937, Series A, Vol.
31. – P. 268-282.
5. Cochran W.G. The
distribution of the largest of a set of estimated variances as a fraction of
their total // Ann. of eugenics, 1941, 11. – P. 47-52.
6. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. – Л.: Энергоатомиздат, 1991. – 303 с.
7. Лемешко Б.Ю., Помадин С.С. Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального // Измерительная техника. 2004. (в печати)
8. Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов. 2002. – 87 с.
9. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. – М.: Изд-во стандартов. 2002. – 64 с.
10. Box G.E.P. Non-normality and tests on variances // Biometrika. 1953. Vol. 40. – P. 318-335.
11. Шеффе Г. Дисперсионный анализ. М.: Физматгиз, 1980. – 628 с.
Приложение
1. Верхние процентные (´100%) точки для статистики (5)
критерия Бартлетта, построенной по m независимым оценкам дисперсии, каждая из которых обладает 
степенями свободы. Выборка
принадлежит распределению экспоненциального семейства с параметром формы 0.5
|
|
|
|
||||
|
0.15 |
0.1 |
0.05 |
0.02 |
0.01 |
||
|
2 |
10 |
8.696 |
10.939 |
14.566 |
18.995 |
22.022 |
|
50 |
14.398 |
18.441 |
25.350 |
34.179 |
40.460 |
|
|
100 |
15.958 |
20.577 |
28.389 |
38.719 |
46.408 |
|
|
3 |
10 |
16.171 |
19.154 |
24.118 |
30.235 |
34.591 |
|
50 |
26.409 |
31.592 |
40.114 |
50.923 |
58.713 |
|
|
100 |
28.854 |
34.664 |
44.376 |
56.351 |
65.263 |
|
|
4 |
10 |
23.277 |
26.993 |
33.024 |
40.476 |
45.464 |
|
50 |
37.134 |
43.203 |
52.957 |
64.867 |
73.391 |
|
|
100 |
40.707 |
47.370 |
58.375 |
71.864 |
82.102 |
|
|
5 |
10 |
29.973 |
34.342 |
41.283 |
49.656 |
55.635 |
|
50 |
47.535 |
54.264 |
64.982 |
78.312 |
87.494 |
|
|
100 |
51.569 |
58.996 |
70.986 |
86.084 |
96.910 |
|
|
6 |
10 |
36.668 |
41.594 |
49.386 |
58.652 |
64.895 |
|
50 |
57.216 |
64.410 |
76.019 |
90.038 |
100.490 |
|
|
100 |
61.923 |
69.856 |
82.460 |
98.508 |
109.961 |
|
|
7 |
10 |
43.170 |
48.439 |
56.918 |
66.787 |
73.452 |
|
50 |
66.746 |
74.484 |
86.958 |
102.256 |
113.151 |
|
|
100 |
72.396 |
80.886 |
94.512 |
111.502 |
123.382 |
|
|
8 |
10 |
49.845 |
55.546 |
64.543 |
75.261 |
82.565 |
|
50 |
76.011 |
84.196 |
97.263 |
113.256 |
124.592 |
|
|
100 |
82.481 |
91.723 |
106.246 |
123.946 |
136.624 |
|
|
9 |
10 |
56.174 |
62.298 |
71.848 |
82.708 |
90.034 |
|
50 |
85.347 |
94.062 |
108.034 |
124.733 |
136.179 |
|
|
100 |
92.070 |
101.661 |
116.739 |
135.901 |
149.048 |
|
|
10 |
10 |
62.403 |
68.915 |
78.809 |
90.654 |
98.478 |
|
50 |
94.255 |
103.387 |
117.872 |
135.062 |
147.106 |
|
|
100 |
102.088 |
112.184 |
128.069 |
147.559 |
161.180 |
|
Приложение
2. Верхние процентные (´100%) точки для статистики (5)
критерия Бартлетта, построенной по m независимым оценкам дисперсии, каждая из которых обладает степенями свободы. Выборка
принадлежит распределению экспоненциального семейства с параметром формы 1 (распределению
Лапласа)
|
|
|
|
||||
|
0.15 |
0.1 |
0.05 |
0.02 |
0.01 |
||
|
2 |
10 |
3.962 |
5.099 |
7.039 |
9.574 |
11.367 |
|
50 |
4.778 |
6.213 |
8.782 |
12.290 |
14.930 |
|
|
100 |
4.923 |
6.419 |
9.069 |
12.701 |
15.425 |
|
|
3 |
10 |
7.253 |
8.707 |
11.162 |
14.272 |
16.513 |
|
50 |
8.782 |
10.625 |
13.740 |
17.786 |
20.797 |
|
|
100 |
8.947 |
10.834 |
14.060 |
18.292 |
21.395 |
|
|
4 |
10 |
10.290 |
11.978 |
14.778 |
18.237 |
20.816 |
|
50 |
12.261 |
14.399 |
17.905 |
22.417 |
25.798 |
|
|
100 |
12.633 |
14.831 |
18.520 |
23.295 |
26.868 |
|
|
5 |
10 |
13.035 |
14.955 |
18.090 |
21.926 |
24.813 |
|
50 |
15.646 |
18.023 |
21.930 |
26.834 |
30.543 |
|
|
100 |
16.045 |
18.472 |
22.477 |
27.694 |
31.540 |
|
|
6 |
10 |
15.752 |
17.854 |
21.230 |
25.432 |
28.485 |
|
50 |
18.747 |
21.308 |
25.506 |
30.755 |
34.633 |
|
|
100 |
19.220 |
21.866 |
26.225 |
31.448 |
35.432 |
|
|
7 |
10 |
18.351 |
20.602 |
24.189 |
28.655 |
31.983 |
|
50 |
21.870 |
24.628 |
29.063 |
34.627 |
38.713 |
|
|
100 |
22.450 |
25.299 |
29.865 |
35.603 |
39.872 |
|
|
8 |
10 |
20.996 |
23.365 |
27.218 |
32.084 |
35.661 |
|
50 |
24.881 |
27.786 |
32.502 |
38.263 |
42.486 |
|
|
100 |
25.588 |
28.577 |
33.406 |
39.498 |
43.765 |
|
|
9 |
10 |
23.529 |
26.059 |
30.053 |
35.102 |
38.648 |
|
50 |
27.884 |
30.958 |
35.896 |
42.091 |
46.435 |
|
|
100 |
28.533 |
31.711 |
36.717 |
43.111 |
47.483 |
|
|
10 |
10 |
26.042 |
28.682 |
32.986 |
38.182 |
41.853 |
|
50 |
30.776 |
33.979 |
39.201 |
45.358 |
49.875 |
|
|
100 |
31.554 |
34.819 |
40.135 |
46.717 |
51.317 |
|
Приложение
3. Верхние процентные (´100%) точки для статистики (5)
критерия Бартлетта, построенной по m независимым оценкам дисперсии, каждая из которых обладает степенями свободы. Выборка
принадлежит распределению экспоненциального семейства с параметром формы 1.5
|
|
|
|
||||
|
0.15 |
0.1 |
0.05 |
0.02 |
0.01 |
||
|
2 |
10 |
2.628 |
3.420 |
4.808 |
6.646 |
8.068 |
|
50 |
2.800 |
3.650 |
5.197 |
7.344 |
8.964 |
|
|
100 |
2.829 |
3.700 |
5.208 |
7.372 |
9.000 |
|
|
3 |
10 |
4.810 |
5.809 |
7.511 |
9.722 |
11.351 |
|
50 |
5.157 |
6.246 |
8.096 |
10.499 |
12.296 |
|
|
100 |
5.133 |
6.210 |
8.079 |
10.525 |
12.409 |
|
|
4 |
10 |
6.785 |
7.950 |
9.874 |
12.268 |
14.066 |
|
50 |
7.182 |
8.420 |
10.496 |
13.211 |
15.197 |
|
|
100 |
7.233 |
8.495 |
10.627 |
13.461 |
15.461 |
|
|
5 |
10 |
8.595 |
9.873 |
11.964 |
14.550 |
16.452 |
|
50 |
9.147 |
10.561 |
12.861 |
15.764 |
17.880 |
|
|
100 |
9.188 |
10.597 |
12.895 |
15.957 |
18.122 |
|
|
6 |
10 |
10.319 |
11.729 |
13.972 |
16.764 |
18.799 |
|
50 |
10.960 |
12.443 |
14.915 |
18.038 |
20.270 |
|
|
100 |
11.032 |
12.519 |
14.988 |
18.062 |
20.324 |
|
|
7 |
10 |
12.007 |
13.473 |
15.880 |
18.859 |
21.052 |
|
50 |
12.756 |
14.380 |
16.984 |
20.227 |
22.641 |
|
|
100 |
12.859 |
14.496 |
17.129 |
20.418 |
22.883 |
|
|
8 |
10 |
13.690 |
15.257 |
17.816 |
20.934 |
23.310 |
|
50 |
14.499 |
16.238 |
18.977 |
22.340 |
24.820 |
|
|
100 |
14.605 |
16.330 |
19.198 |
22.653 |
25.144 |
|
|
9 |
10 |
15.319 |
16.997 |
19.640 |
22.891 |
25.239 |
|
50 |
16.284 |
18.066 |
20.933 |
24.516 |
27.224 |
|
|
100 |
16.346 |
18.158 |
21.054 |
24.683 |
27.258 |
|
|
10 |
10 |
16.946 |
18.680 |
21.451 |
24.802 |
27.241 |
|
50 |
17.940 |
19.789 |
22.814 |
26.486 |
29.123 |
|
|
100 |
18.071 |
19.977 |
23.023 |
26.796 |
29.535 |
|
Приложение
4. Верхние процентные (´100%) точки для статистики (5)
критерия Бартлетта, построенной по m независимым оценкам дисперсии, каждая из которых обладает степенями свободы. Выборка
принадлежит распределению экспоненциального семейства с параметром формы 3
|
|
|
|
||||
|
0.15 |
0.1 |
0.05 |
0.02 |
0.01 |
||
|
2 |
10 |
1.588 |
2.093 |
3.015 |
4.297 |
5.343 |
|
50 |
1.487 |
1.948 |
2.791 |
3.968 |
4.895 |
|
|
100 |
1.486 |
1.936 |
2.752 |
3.890 |
4.772 |
|
|
3 |
10 |
2.913 |
3.552 |
4.688 |
6.198 |
7.061 |
|
50 |
2.739 |
3.327 |
4.331 |
5.669 |
6.636 |
|
|
100 |
2.699 |
3.263 |
4.244 |
5.564 |
6.570 |
|
|
4 |
10 |
4.109 |
4.865 |
6.127 |
7.828 |
9.070 |
|
50 |
3.819 |
4.490 |
5.631 |
7.120 |
8.266 |
|
|
100 |
3.784 |
4.453 |
5.602 |
7.081 |
8.176 |
|
|
5 |
10 |
5.194 |
6.032 |
7.417 |
9.204 |
10.518 |
|
50 |
4.874 |
5.635 |
6.902 |
8.481 |
9.673 |
|
|
100 |
4.811 |
5.554 |
6.778 |
8.401 |
9.611 |
|
|
6 |
10 |
6.248 |
7.143 |
8.659 |
10.562 |
11.954 |
|
50 |
5.833 |
6.640 |
7.964 |
9.672 |
10.911 |
|
|
100 |
5.778 |
6.570 |
7.890 |
9.532 |
10.737 |
|
|
7 |
10 |
7.271 |
8.213 |
9.790 |
11.801 |
13.300 |
|
50 |
6.792 |
7.669 |
9.108 |
10.901 |
12.199 |
|
|
100 |
6.738 |
7.609 |
9.012 |
10.795 |
12.079 |
|
|
8 |
10 |
8.272 |
9.289 |
10.942 |
13.021 |
14.571 |
|
50 |
7.735 |
8.647 |
10.155 |
12.008 |
13.382 |
|
|
100 |
7.680 |
8.600 |
10.085 |
11.922 |
13.241 |
|
|
9 |
10 |
9.260 |
10.339 |
12.091 |
14.278 |
15.829 |
|
50 |
8.676 |
9.647 |
11.203 |
13.156 |
14.558 |
|
|
100 |
8.565 |
9.513 |
11.054 |
12.965 |
14.347 |
|
|
10 |
10 |
10.233 |
11.343 |
13.116 |
15.347 |
16.946 |
|
50 |
9.559 |
10.557 |
12.189 |
14.204 |
15.633 |
|
|
100 |
9.470 |
10.461 |
12.068 |
14.098 |
15.582 |
|
Приложение
5. Верхние процентные (´100%) точки для статистики (5)
критерия Бартлетта, построенной по m независимым оценкам дисперсии, каждая из которых обладает степенями свободы. Выборка
принадлежит распределению экспоненциального семейства с параметром формы 4
|
|
|
|
||||
|
0.15 |
0.1 |
0.05 |
0.02 |
0.01 |
||
|
2 |
10 |
1.386 |
1.837 |
2.664 |
3.854 |
4.817 |
|
50 |
1.257 |
1.646 |
2.361 |
3.363 |
4.159 |
|
|
100 |
1.246 |
1.631 |
2.317 |
3.262 |
4.020 |
|
|
3 |
10 |
2.553 |
3.126 |
4.155 |
5.540 |
6.627 |
|
50 |
2.317 |
2.812 |
3.669 |
4.801 |
5.645 |
|
|
100 |
2.266 |
2.753 |
3.571 |
4.678 |
5.542 |
|
|
4 |
10 |
3.605 |
4.280 |
5.432 |
7.009 |
8.142 |
|
50 |
3.220 |
3.801 |
4.772 |
6.044 |
6.995 |
|
|
100 |
3.186 |
3.752 |
4.717 |
5.955 |
6.884 |
|
|
5 |
10 |
4.563 |
5.316 |
6.579 |
8.229 |
9.443 |
|
50 |
4.116 |
4.761 |
5.839 |
7.184 |
8.205 |
|
|
100 |
4.040 |
4.670 |
5.718 |
7.091 |
8.107 |
|
|
6 |
10 |
5.491 |
6.296 |
7.674 |
9.429 |
10.727 |
|
50 |
4.926 |
5.618 |
6.743 |
8.199 |
9.245 |
|
|
100 |
4.865 |
5.532 |
6.644 |
8.044 |
9.068 |
|
|
7 |
10 |
6.382 |
7.236 |
8.677 |
10.537 |
11.951 |
|
50 |
5.738 |
6.485 |
7.704 |
9.238 |
10.329 |
|
|
100 |
5.670 |
6.403 |
7.596 |
9.090 |
10.159 |
|
|
8 |
10 |
7.263 |
8.196 |
9.687 |
11.615 |
13.042 |
|
50 |
6.538 |
7.311 |
8.593 |
10.179 |
11.347 |
|
|
100 |
6.457 |
7.234 |
8.476 |
10.050 |
11.171 |
|
|
9 |
10 |
8.130 |
9.110 |
10.698 |
12.694 |
13.778 |
|
50 |
7.330 |
8.153 |
9.484 |
11.144 |
12.352 |
|
|
100 |
7.207 |
8.024 |
9.333 |
10.948 |
12.101 |
|
|
10 |
10 |
8.986 |
9.989 |
11.605 |
13.671 |
15.141 |
|
50 |
8.073 |
8.930 |
10.319 |
12.048 |
13.260 |
|
|
100 |
7.965 |
8.812 |
10.174 |
11.851 |
13.098 |
|
Приложение
6. Верхние процентные (´100%) точки для статистики (5)
критерия Бартлетта, построенной по m независимым оценкам дисперсии, каждая из которых обладает степенями свободы. Выборка
принадлежит распределению экспоненциального семейства с параметром формы 5
|
|
|
|
||||
|
0.15 |
0.1 |
0.05 |
0.02 |
0.01 |
||
|
2 |
10 |
1.280 |
1.704 |
2.489 |
3.619 |
4.525 |
|
50 |
1.135 |
1.491 |
2.138 |
3.055 |
3.780 |
|
|
100 |
1.124 |
1.472 |
2.095 |
2.945 |
3.634 |
|
|
3 |
10 |
2.363 |
2.905 |
3.871 |
5.204 |
6.000 |
|
50 |
2.094 |
2.546 |
3.325 |
4.354 |
5.125 |
|
|
100 |
2.048 |
2.489 |
3.228 |
4.228 |
5.021 |
|
|
4 |
10 |
3.340 |
3.979 |
5.072 |
6.594 |
7.699 |
|
50 |
2.911 |
3.442 |
4.320 |
5.473 |
6.343 |
|
|
100 |
2.876 |
3.388 |
4.260 |
5.382 |
6.227 |
|
|
5 |
10 |
4.234 |
4.942 |
6.146 |
7.726 |
7.717 |
|
50 |
3.727 |
4.312 |
5.041 |
6.511 |
7.451 |
|
|
100 |
3.652 |
4.214 |
5.173 |
6.414 |
7.312 |
|
|
6 |
10 |
5.093 |
5.860 |
7.171 |
8.837 |
10.112 |
|
50 |
4.459 |
5.084 |
6.109 |
7.421 |
8.404 |
|
|
100 |
4.391 |
4.991 |
6.004 |
7.265 |
8.188 |
|
|
7 |
10 |
5.920 |
6.728 |
8.099 |
9.882 |
11.234 |
|
50 |
5.209 |
5.886 |
6.980 |
8.382 |
9.355 |
|
|
100 |
5.122 |
5.780 |
6.864 |
8.208 |
9.183 |
|
|
8 |
10 |
6.741 |
7.616 |
8.685 |
10.883 |
12.242 |
|
50 |
5.914 |
6.623 |
7.790 |
9.217 |
10.312 |
|
|
100 |
5.839 |
6.547 |
7.666 |
9.072 |
10.079 |
|
|
9 |
10 |
7.545 |
8.469 |
9.976 |
11.904 |
13.297 |
|
50 |
6.630 |
7.385 |
8.604 |
9.721 |
11.215 |
|
|
100 |
6.500 |
7.241 |
8.433 |
9.884 |
10.910 |
|
|
10 |
10 |
8.336 |
9.287 |
10.831 |
12.800 |
14.202 |
|
50 |
7.315 |
8.098 |
9.369 |
10.928 |
12.035 |
|
|
100 |
7.208 |
7.970 |
9.208 |
10.729 |
11.819 |
|
Приложение
7. Верхние процентные (´100%) точки для статистики (5)
критерия Бартлетта, построенной по m независимым оценкам дисперсии, каждая из которых обладает степенями свободы. Выборка
принадлежит распределению экспоненциального семейства с параметром формы 10
|
|
|
|
||||
|
0.15 |
0.1 |
0.05 |
0.02 |
0.01 |
||
|
2 |
10 |
1.115 |
1.493 |
2.206 |
3.255 |
4.118 |
|
50 |
0.950 |
1.244 |
1.789 |
2.567 |
3.157 |
|
|
100 |
0.933 |
1.221 |
1.741 |
2.460 |
3.019 |
|
|
3 |
10 |
2.063 |
2.552 |
3.442 |
4.687 |
5.671 |
|
50 |
1.747 |
2.126 |
2.776 |
3.645 |
4.308 |
|
|
100 |
1.701 |
2.069 |
2.690 |
3.515 |
4.182 |
|
|
4 |
10 |
2.919 |
3.502 |
4.522 |
5.939 |
7.008 |
|
50 |
2.437 |
2.885 |
3.624 |
4.587 |
5.321 |
|
|
100 |
2.385 |
2.815 |
3.537 |
4.485 |
5.188 |
|
|
5 |
10 |
3.711 |
4.354 |
5.474 |
6.957 |
8.070 |
|
50 |
3.112 |
3.602 |
4.414 |
5.458 |
6.246 |
|
|
100 |
3.030 |
3.500 |
4.305 |
5.336 |
6.079 |
|
|
6 |
10 |
4.468 |
5.173 |
6.382 |
7.952 |
9.169 |
|
50 |
3.718 |
4.246 |
5.115 |
6.222 |
7.055 |
|
|
100 |
3.653 |
4.166 |
5.008 |
6.055 |
6.829 |
|
|
7 |
10 |
5.199 |
5.939 |
7.209 |
8.905 |
10.165 |
|
50 |
4.340 |
4.911 |
5.837 |
7.031 |
7.876 |
|
|
100 |
4.253 |
4.803 |
5.709 |
6.842 |
7.673 |
|
|
8 |
10 |
5.911 |
6.513 |
8.054 |
9.775 |
11.075 |
|
50 |
4.938 |
5.533 |
6.515 |
7.730 |
8.633 |
|
|
100 |
4.844 |
5.429 |
6.361 |
7.521 |
8.357 |
|
|
9 |
10 |
6.638 |
7.464 |
8.873 |
10.663 |
12.018 |
|
50 |
5.548 |
6.176 |
7.198 |
8.498 |
9.214 |
|
|
100 |
5.397 |
6.023 |
7.018 |
8.227 |
9.116 |
|
|
10 |
10 |
7.317 |
8.181 |
9.622 |
11.487 |
12.813 |
|
50 |
6.118 |
6.764 |
7.831 |
9.167 |
10.065 |
|
|
100 |
5.981 |
6.617 |
7.639 |
8.909 |
9.813 |
|
Приложение 8. Верхние процентные (1%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 0.5
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.99998 |
0.9993 |
0.9977 |
0.9960 |
0.9941 |
0.9913 |
0.9871 |
0.9833 |
0.9796 |
0.9769 |
0.9568 |
0.9001 |
0.7625 |
|
3 |
0.9990 |
0.9925 |
0.9857 |
0.9758 |
0.9688 |
0.9588 |
0.9492 |
0.9413 |
0.9329 |
0.9287 |
0.8862 |
0.7798 |
0.5967 |
|
4 |
0.9938 |
0.9821 |
0.9653 |
0.9573 |
0.9370 |
0.9245 |
0.9041 |
0.8927 |
0.8806 |
0.8755 |
0.8133 |
0.6853 |
0.4790 |
|
5 |
0.9864 |
0.9690 |
0.9483 |
0.9271 |
0.9095 |
0.8799 |
0.8658 |
0.8513 |
0.8357 |
0.8262 |
0.7502 |
0.6009 |
0.4103 |
|
6 |
0.9806 |
0.9476 |
0.9241 |
0.8950 |
0.8706 |
0.8512 |
0.8294 |
0.8149 |
0.7989 |
0.7691 |
0.6850 |
0.5345 |
0.3475 |
|
7 |
0.9682 |
0.9338 |
0.8998 |
0.8695 |
0.8387 |
0.8160 |
0.8059 |
0.7740 |
0.7513 |
0.7284 |
0.6421 |
0.4909 |
0.3139 |
|
8 |
0.9591 |
0.9208 |
0.8772 |
0.8489 |
0.8115 |
0.7997 |
0.7628 |
0.7391 |
0.7187 |
0.7013 |
0.6021 |
0.4470 |
0.2729 |
|
9 |
0.9470 |
0.9065 |
0.8585 |
0.8208 |
0.7958 |
0.7610 |
0.7366 |
0.7039 |
0.6877 |
0.6635 |
0.5640 |
0.4186 |
0.2501 |
|
10 |
0.9403 |
0.8964 |
0.8398 |
0.8023 |
0.7674 |
0.7347 |
0.6987 |
0.6769 |
0.6533 |
0.6187 |
0.5398 |
0.3885 |
0.2264 |
|
12 |
0.9207 |
0.8513 |
0.8048 |
0.7661 |
0.7201 |
0.6880 |
0.6541 |
0.6200 |
0.5984 |
0.5806 |
0.4823 |
0.3467 |
0.1949 |
|
15 |
0.8861 |
0.8148 |
0.7591 |
0.7078 |
0.6588 |
0.6141 |
0.5900 |
0.5595 |
0.5333 |
0.5173 |
0.4159 |
0.2857 |
0.1615 |
|
20 |
0.8369 |
0.7592 |
0.6760 |
0.6170 |
0.5801 |
0.5386 |
0.5055 |
0.4791 |
0.4486 |
0.4323 |
0.3406 |
0.2262 |
0.1249 |
|
24 |
0.7902 |
0.7131 |
0.6337 |
0.5790 |
0.5238 |
0.4794 |
0.4560 |
0.4229 |
0.4042 |
0.3857 |
0.2978 |
0.1960 |
0.1058 |
|
30 |
0.7439 |
0.6542 |
0.5693 |
0.5094 |
0.4682 |
0.4133 |
0.3932 |
0.3652 |
0.3452 |
0.3270 |
0.2516 |
0.1627 |
0.0873 |
|
40 |
0.6696 |
0.5729 |
0.4866 |
0.4209 |
0.3843 |
0.3507 |
0.3181 |
0.2933 |
0.2741 |
0.2650 |
0.1987 |
0.1287 |
0.0665 |
|
60 |
0.5682 |
0.4550 |
0.3800 |
0.3330 |
0.2835 |
0.2513 |
0.2373 |
0.2112 |
0.2008 |
0.1947 |
0.1410 |
0.0900 |
0.0465 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 9. Верхние процентные (1%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 1 (распределению Лапласа)
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.99995 |
0.9972 |
0.9898 |
0.9782 |
0.9749 |
0.9647 |
0.9488 |
0.9387 |
0.9264 |
0.9174 |
0.8717 |
0.7856 |
0.6594 |
|
3 |
0.9970 |
0.9695 |
0.9407 |
0.9079 |
0.8856 |
0.8659 |
0.8413 |
0.8269 |
0.8083 |
0.7908 |
0.7240 |
0.6063 |
0.4746 |
|
4 |
0.9813 |
0.9312 |
0.8807 |
0.8551 |
0.8002 |
0.7869 |
0.7438 |
0.7337 |
0.7036 |
0.7104 |
0.6117 |
0.4991 |
0.3723 |
|
5 |
0.9532 |
0.8884 |
0.8285 |
0.7748 |
0.7345 |
0.6996 |
0.6721 |
0.6549 |
0.6350 |
0.6222 |
0.5378 |
0.4154 |
0.3066 |
|
6 |
0.9360 |
0.8358 |
0.7648 |
0.7296 |
0.6759 |
0.6381 |
0.6147 |
0.5934 |
0.5764 |
0.5519 |
0.4695 |
0.3634 |
0.2590 |
|
7 |
0.8969 |
0.7964 |
0.7267 |
0.6780 |
0.6194 |
0.5916 |
0.5780 |
0.5495 |
0.5210 |
0.5051 |
0.4196 |
0.3250 |
0.2282 |
|
8 |
0.8744 |
0.7718 |
0.6825 |
0.6241 |
0.5767 |
0.5553 |
0.5204 |
0.4987 |
0.4712 |
0.4566 |
0.3799 |
0.2874 |
0.2019 |
|
9 |
0.8461 |
0.7313 |
0.6544 |
0.5959 |
0.5496 |
0.5097 |
0.4848 |
0.4532 |
0.4403 |
0.4240 |
0.3421 |
0.2632 |
0.1802 |
|
10 |
0.8237 |
0.7147 |
0.6092 |
0.5530 |
0.5106 |
0.4792 |
0.4496 |
0.4251 |
0.4063 |
0.3937 |
0.3222 |
0.2415 |
0.1637 |
|
12 |
0.7737 |
0.6479 |
0.5654 |
0.5006 |
0.4575 |
0.4274 |
0.3959 |
0.3770 |
0.3608 |
0.3470 |
0.2815 |
0.2093 |
0.1378 |
|
15 |
0.7159 |
0.5770 |
0.4959 |
0.4504 |
0.3936 |
0.3656 |
0.3396 |
0.3275 |
0.3043 |
0.2967 |
0.2418 |
0.1759 |
0.1125 |
|
20 |
0.6235 |
0.5008 |
0.4078 |
0.3552 |
0.3269 |
0.3028 |
0.2793 |
0.2689 |
0.2508 |
0.2386 |
0.1897 |
0.1340 |
0.0857 |
|
24 |
0.5715 |
0.4414 |
0.3686 |
0.3195 |
0.2945 |
0.2631 |
0.2454 |
0.2302 |
0.2180 |
0.2072 |
0.1638 |
0.1151 |
0.0723 |
|
30 |
0.5117 |
0.3833 |
0.3154 |
0.2743 |
0.2569 |
0.2184 |
0.2061 |
0.1969 |
0.1840 |
0.1727 |
0.1368 |
0.0942 |
0.0587 |
|
40 |
0.4277 |
0.3211 |
0.2583 |
0.2214 |
0.1999 |
0.1838 |
0.1632 |
0.1538 |
0.1430 |
0.1366 |
0.1055 |
0.0733 |
0.0451 |
|
60 |
0.3311 |
0.2462 |
0.1941 |
0.1671 |
0.1437 |
0.1283 |
0.1176 |
0.1063 |
0.1034 |
0.0971 |
0.0738 |
0.0503 |
0.0306 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 10. Верхние процентные (1%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 3
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.99992 |
0.9932 |
0.9768 |
0.9423 |
0.9251 |
0.9058 |
0.8711 |
0.8572 |
0.8376 |
0.8208 |
0.7615 |
0.6745 |
0.5907 |
|
3 |
0.9919 |
0.9265 |
0.8598 |
0.7900 |
0.7576 |
0.7176 |
0.6873 |
0.6635 |
0.6535 |
0.6355 |
0.5667 |
0.4847 |
0.4059 |
|
4 |
0.9636 |
0.8446 |
0.7412 |
0.6666 |
0.6250 |
0.5947 |
0.5644 |
0.5576 |
0.5159 |
0.5134 |
0.4497 |
0.3780 |
0.3122 |
|
5 |
0.9286 |
0.7671 |
0.6341 |
0.5824 |
0.5364 |
0.4985 |
0.4757 |
0.4593 |
0.4410 |
0.4310 |
0.3683 |
0.3085 |
0.2545 |
|
6 |
0.8650 |
0.6769 |
0.5620 |
0.5027 |
0.4581 |
0.4415 |
0.4142 |
0.3961 |
0.3750 |
0.3682 |
0.3164 |
0.2644 |
0.2132 |
|
7 |
0.8121 |
0.6133 |
0.5214 |
0.4562 |
0.4091 |
0.3871 |
0.3659 |
0.3446 |
0.3310 |
0.3222 |
0.2779 |
0.2308 |
0.1843 |
|
8 |
0.7690 |
0.5504 |
0.4606 |
0.4069 |
0.3635 |
0.3460 |
0.3239 |
0.3118 |
0.2974 |
0.2862 |
0.2458 |
0.2039 |
0.1624 |
|
9 |
0.7170 |
0.5137 |
0.4243 |
0.3743 |
0.3364 |
0.3143 |
0.2977 |
0.2742 |
0.2694 |
0.2579 |
0.2197 |
0.1819 |
0.1448 |
|
10 |
0.6610 |
0.4745 |
0.3914 |
0.3393 |
0.3071 |
0.2883 |
0.2723 |
0.2548 |
0.2454 |
0.2354 |
0.2002 |
0.1648 |
0.1307 |
|
12 |
0.6027 |
0.4231 |
0.3329 |
0.2925 |
0.2636 |
0.2454 |
0.2316 |
0.2144 |
0.2106 |
0.2013 |
0.1712 |
0.1389 |
0.1101 |
|
15 |
0.5215 |
0.3431 |
0.2783 |
0.2452 |
0.2146 |
0.2045 |
0.1911 |
0.1781 |
0.1715 |
0.1662 |
0.1414 |
0.1132 |
0.0888 |
|
20 |
0.4156 |
0.2791 |
0.2191 |
0.1883 |
0.1714 |
0.1567 |
0.1483 |
0.1384 |
0.1324 |
0.1272 |
0.1075 |
0.0861 |
0.0671 |
|
24 |
0.3641 |
0.2341 |
0.1848 |
0.1615 |
0.1437 |
0.1321 |
0.1246 |
0.1157 |
0.1125 |
0.1082 |
0.0919 |
0.0727 |
0.0562 |
|
30 |
0.3059 |
0.1929 |
0.1541 |
0.1343 |
0.1192 |
0.1093 |
0.1030 |
0.0956 |
0.0921 |
0.0874 |
0.0743 |
0.0591 |
0.0452 |
|
40 |
0.2417 |
0.1509 |
0.1200 |
0.1026 |
0.0911 |
0.0839 |
0.0776 |
0.0730 |
0.0712 |
0.0679 |
0.0569 |
0.0448 |
0.0341 |
|
60 |
0.1685 |
0.1069 |
0.0831 |
0.0716 |
0.0628 |
0.0574 |
0.0531 |
0.0500 |
0.0492 |
0.0460 |
0.0388 |
0.0307 |
0.0229 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 11. Верхние процентные (1%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 5
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.99991 |
0.9931 |
0.9751 |
0.9354 |
0.9155 |
0.8881 |
0.8565 |
0.8393 |
0.8172 |
0.7993 |
0.7396 |
0.6556 |
0.5778 |
|
3 |
0.9945 |
0.9309 |
0.8341 |
0.7670 |
0.7355 |
0.6945 |
0.6568 |
0.6320 |
0.6225 |
0.6075 |
0.5416 |
0.4645 |
0.3961 |
|
4 |
0.9651 |
0.8351 |
0.7114 |
0.6444 |
0.5889 |
0.5577 |
0.5313 |
0.5227 |
0.4861 |
0.4819 |
0.4225 |
0.3616 |
0.3040 |
|
5 |
0.9135 |
0.7327 |
0.5969 |
0.5378 |
0.4998 |
0.4653 |
0.4402 |
0.4246 |
0.4074 |
0.3965 |
0.3451 |
0.2932 |
0.2468 |
|
6 |
0.8597 |
0.6521 |
0.5211 |
0.4730 |
0.4234 |
0.4024 |
0.3825 |
0.3631 |
0.3466 |
0.3392 |
0.2953 |
0.2496 |
0.2066 |
|
7 |
0.7989 |
0.5680 |
0.4686 |
0.4105 |
0.3757 |
0.3538 |
0.3305 |
0.3179 |
0.3053 |
0.2942 |
0.2579 |
0.2170 |
0.1785 |
|
8 |
0.7498 |
0.5277 |
0.4166 |
0.3659 |
0.3320 |
0.3130 |
0.2935 |
0.2843 |
0.2724 |
0.2604 |
0.2284 |
0.1904 |
0.1571 |
|
9 |
0.6913 |
0.4775 |
0.3765 |
0.3382 |
0.3028 |
0.2831 |
0.2716 |
0.2511 |
0.2443 |
0.2352 |
0.2053 |
0.1711 |
0.1398 |
|
10 |
0.6514 |
0.4488 |
0.3402 |
0.3070 |
0.2727 |
0.2576 |
0.2461 |
0.2293 |
0.2230 |
0.2134 |
0.1846 |
0.1551 |
0.1265 |
|
12 |
0.5688 |
0.3764 |
0.2945 |
0.2564 |
0.2331 |
0.2199 |
0.2081 |
0.1943 |
0.1907 |
0.1804 |
0.1581 |
0.1301 |
0.1063 |
|
15 |
0.4868 |
0.3034 |
0.2416 |
0.2148 |
0.1910 |
0.1800 |
0.1721 |
0.1581 |
0.1530 |
0.1488 |
0.1283 |
0.1056 |
0.0854 |
|
20 |
0.3774 |
0.2415 |
0.1877 |
0.1643 |
0.1487 |
0.1386 |
0.1316 |
0.1219 |
0.1189 |
0.1131 |
0.0986 |
0.0806 |
0.0645 |
|
24 |
0.3301 |
0.2017 |
0.1609 |
0.1395 |
0.1265 |
0.1164 |
0.1092 |
0.1040 |
0.0993 |
0.0950 |
0.0833 |
0.0674 |
0.0541 |
|
30 |
0.2694 |
0.1616 |
0.1298 |
0.1153 |
0.1027 |
0.0946 |
0.0904 |
0.0850 |
0.0814 |
0.0773 |
0.0669 |
0.0546 |
0.0434 |
|
40 |
0.2093 |
0.1271 |
0.1017 |
0.0874 |
0.0782 |
0.0729 |
0.0681 |
0.0641 |
0.0624 |
0.0596 |
0.0511 |
0.0415 |
0.0327 |
|
60 |
0.1409 |
0.0865 |
0.0693 |
0.0600 |
0.0538 |
0.0494 |
0.0464 |
0.0438 |
0.0428 |
0.0408 |
0.0346 |
0.0284 |
0.0220 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 12. Верхние процентные (1%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 10
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.99991 |
0.9926 |
0.9743 |
0.9320 |
0.9113 |
0.8783 |
0.8466 |
0.8287 |
0.8053 |
0.7861 |
0.7258 |
0.6451 |
0.5707 |
|
3 |
0.9944 |
0.9257 |
0.8253 |
0.7540 |
0.7186 |
0.6789 |
0.6368 |
0.6136 |
0.6008 |
0.5849 |
0.5253 |
0.4530 |
0.3904 |
|
4 |
0.9656 |
0.8267 |
0.6875 |
0.6199 |
0.5657 |
0.5344 |
0.5124 |
0.4977 |
0.4694 |
0.4627 |
0.4072 |
0.3505 |
0.2985 |
|
5 |
0.9149 |
0.7169 |
0.5791 |
0.5140 |
0.4757 |
0.4439 |
0.4213 |
0.4060 |
0.3888 |
0.3791 |
0.3339 |
0.2839 |
0.2419 |
|
6 |
0.8588 |
0.6383 |
0.5001 |
0.4491 |
0.4037 |
0.3817 |
0.3594 |
0.3448 |
0.3290 |
0.3214 |
0.2837 |
0.2420 |
0.2032 |
|
7 |
0.7908 |
0.5505 |
0.4455 |
0.3872 |
0.3523 |
0.3325 |
0.3148 |
0.3021 |
0.2892 |
0.2791 |
0.2445 |
0.2089 |
0.1751 |
|
8 |
0.7414 |
0.4978 |
0.3960 |
0.3411 |
0.3135 |
0.2923 |
0.2780 |
0.2674 |
0.2567 |
0.2479 |
0.2180 |
0.1836 |
0.1538 |
|
9 |
0.6791 |
0.4513 |
0.3568 |
0.3150 |
0.2837 |
0.2666 |
0.2535 |
0.2391 |
0.2295 |
0.2209 |
0.1948 |
0.1643 |
0.1368 |
|
10 |
0.6285 |
0.4168 |
0.3186 |
0.2846 |
0.2541 |
0.2418 |
0.2297 |
0.2151 |
0.2094 |
0.2010 |
0.1368 |
0.1491 |
0.1238 |
|
12 |
0.5526 |
0.3504 |
0.2725 |
0.2385 |
0.2184 |
0.2036 |
0.1921 |
0.1818 |
0.1763 |
0.1698 |
0.1498 |
0.1246 |
0.1041 |
|
15 |
0.4615 |
0.2823 |
0.2217 |
0.1960 |
0.1774 |
0.1656 |
0.1582 |
0.1476 |
0.1437 |
0.1391 |
0.1209 |
0.1018 |
0.0839 |
|
20 |
0.3556 |
0.2183 |
0.1727 |
0.1497 |
0.1363 |
0.1283 |
0.1211 |
0.1134 |
0.1099 |
0.1049 |
0.0928 |
0.0773 |
0.0630 |
|
24 |
0.3079 |
0.1806 |
0.1443 |
0.1270 |
0.1150 |
0.1079 |
0.1010 |
0.0955 |
0.0918 |
0.0888 |
0.0781 |
0.0647 |
0.0528 |
|
30 |
0.2475 |
0.1422 |
0.1166 |
0.1036 |
0.0935 |
0.0863 |
0.0824 |
0.0776 |
0.0746 |
0.0713 |
0.0629 |
0.0522 |
0.0423 |
|
40 |
0.1856 |
0.1110 |
0.0898 |
0.0782 |
0.0711 |
0.0664 |
0.0623 |
0.0588 |
0.0571 |
0.0548 |
0.0478 |
0.0396 |
0.0319 |
|
60 |
0.1231 |
0.0737 |
0.0615 |
0.0536 |
0.0480 |
0.0448 |
0.0422 |
0.0399 |
0.0394 |
0.0374 |
0.0323 |
0.0269 |
0.0214 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 13. Верхние процентные (5%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 0.5
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9996 |
0.9957 |
0.9900 |
0.9841 |
0.9777 |
0.9716 |
0.9625 |
0.9596 |
0.9544 |
0.9479 |
0.9180 |
0.8473 |
0.7150 |
|
3 |
0.9918 |
0.9718 |
0.9571 |
0.9383 |
0.9195 |
0.9061 |
0.8985 |
0.8898 |
0.8717 |
0.8543 |
0.8066 |
0.6999 |
0.5347 |
|
4 |
0.9756 |
0.9388 |
0.9123 |
0.8915 |
0.8663 |
0.8462 |
0.8250 |
0.8093 |
0.7976 |
0.7938 |
0.7228 |
0.6039 |
0.4325 |
|
5 |
0.9589 |
0.9122 |
0.8723 |
0.8384 |
0.8192 |
0.7954 |
0.7770 |
0.7587 |
0.7435 |
0.7220 |
0.6650 |
0.5321 |
0.3604 |
|
6 |
0.9348 |
0.8840 |
0.8301 |
0.8046 |
0.7786 |
0.7589 |
0.7310 |
0.7133 |
0.7020 |
0.6853 |
0.6056 |
0.4716 |
0.3093 |
|
7 |
0.9128 |
0.8517 |
0.8203 |
0.7732 |
0.7454 |
0.7197 |
0.7004 |
0.6809 |
0.6590 |
0.6424 |
0.5564 |
0.4183 |
0.2758 |
|
8 |
0.8957 |
0.8280 |
0.7740 |
0.7473 |
0.7180 |
0.6829 |
0.6687 |
0.6322 |
0.6218 |
0.5999 |
0.5154 |
0.3880 |
0.2448 |
|
9 |
0.8789 |
0.8095 |
0.7578 |
0.7204 |
0.6837 |
0.6535 |
0.6262 |
0.6092 |
0.5916 |
0.5648 |
0.4897 |
0.3562 |
0.2232 |
|
10 |
0.8567 |
0.7785 |
0.7362 |
0.6853 |
0.6564 |
0.6346 |
0.5946 |
0.5882 |
0.5592 |
0.5354 |
0.4530 |
0.3308 |
0.2042 |
|
12 |
0.8329 |
0.7473 |
0.6871 |
0.6446 |
0.6139 |
0.5768 |
0.5538 |
0.5306 |
0.5097 |
0.4932 |
0.4069 |
0.2867 |
0.1735 |
|
15 |
0.7835 |
0.7001 |
0.6381 |
0.5990 |
0.5543 |
0.5261 |
0.4975 |
0.4804 |
0.4576 |
0.4334 |
0.3517 |
0.2433 |
0.1432 |
|
20 |
0.7260 |
0.6268 |
0.5744 |
0.5326 |
0.4815 |
0.4560 |
0.4235 |
0.4048 |
0.3842 |
0.3661 |
0.2881 |
0.1929 |
0.1103 |
|
24 |
0.6851 |
0.5848 |
0.5352 |
0.4774 |
0.4446 |
0.4131 |
0.3834 |
0.3623 |
0.3393 |
0.3230 |
0.2507 |
0.1673 |
0.0937 |
|
30 |
0.6359 |
0.5394 |
0.4744 |
0.4268 |
0.3860 |
0.3585 |
0.3299 |
0.3126 |
0.2936 |
0.2731 |
0.2112 |
0.1386 |
0.0778 |
|
40 |
0.5650 |
0.4765 |
0.4023 |
0.3601 |
0.3266 |
0.2987 |
0.2712 |
0.2514 |
0.2346 |
0.2236 |
0.1669 |
0.1088 |
0.0601 |
|
60 |
0.4646 |
0.3787 |
0.3204 |
0.2767 |
0.2457 |
0.2159 |
0.1984 |
0.1840 |
0.1710 |
0.1606 |
0.1193 |
0.0772 |
0.0417 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 14. Верхние процентные (5%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 1 (распределению Лапласа)
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9990 |
0.9843 |
0.9658 |
0.9472 |
0.9282 |
0.9096 |
0.8938 |
0.8850 |
0.8703 |
0.8622 |
0.8154 |
0.7279 |
0.6230 |
|
3 |
0.9782 |
0.9238 |
0.8789 |
0.8423 |
0.8039 |
0.7838 |
0.7595 |
0.7395 |
0.7248 |
0.7095 |
0.6414 |
0.5478 |
0.4432 |
|
4 |
0.9377 |
0.8520 |
0.8030 |
0.7467 |
0.7061 |
0.6786 |
0.6577 |
0.6351 |
0.6234 |
0.6042 |
0.5335 |
0.4473 |
0.3459 |
|
5 |
0.8939 |
0.7880 |
0.7173 |
0.6830 |
0.6465 |
0.6063 |
0.5845 |
0.5574 |
0.5471 |
0.5236 |
0.4656 |
0.3769 |
0.2835 |
|
6 |
0.8569 |
0.7367 |
0.6624 |
0.6157 |
0.5702 |
0.5506 |
0.5256 |
0.4953 |
0.4822 |
0.4636 |
0.4073 |
0.3265 |
0.2388 |
|
7 |
0.8107 |
0.6898 |
0.6200 |
0.5704 |
0.5302 |
0.4999 |
0.4810 |
0.4544 |
0.4354 |
0.4205 |
0.3642 |
0.2825 |
0.2100 |
|
8 |
0.7651 |
0.6497 |
0.5707 |
0.5294 |
0.4924 |
0.4596 |
0.4330 |
0.4157 |
0.3979 |
0.3893 |
0.3330 |
0.2555 |
0.1853 |
|
9 |
0.7358 |
0.6090 |
0.5466 |
0.5009 |
0.4524 |
0.4314 |
0.4066 |
0.3899 |
0.3709 |
0.3569 |
0.3032 |
0.2326 |
0.1667 |
|
10 |
0.7103 |
0.5781 |
0.5112 |
0.4646 |
0.4261 |
0.3983 |
0.3794 |
0.3589 |
0.3440 |
0.3295 |
0.2758 |
0.2144 |
0.1518 |
|
12 |
0.6517 |
0.5312 |
0.4606 |
0.4146 |
0.3792 |
0.3529 |
0.3333 |
0.3186 |
0.3057 |
0.2960 |
0.2440 |
0.1819 |
0.1283 |
|
15 |
0.5902 |
0.4659 |
0.4061 |
0.3565 |
0.3289 |
0.3062 |
0.2845 |
0.2758 |
0.2621 |
0.2464 |
0.2035 |
0.1511 |
0.1044 |
|
20 |
0.5075 |
0.3937 |
0.3401 |
0.2969 |
0.2686 |
0.2511 |
0.2337 |
0.2197 |
0.2076 |
0.2000 |
0.1627 |
0.1174 |
0.0795 |
|
24 |
0.4611 |
0.3477 |
0.3041 |
0.2638 |
0.2405 |
0.2218 |
0.2065 |
0.1908 |
0.1823 |
0.1720 |
0.1388 |
0.1002 |
0.0671 |
|
30 |
0.4006 |
0.3067 |
0.2583 |
0.2244 |
0.2020 |
0.1865 |
0.1701 |
0.1634 |
0.1532 |
0.1459 |
0.1146 |
0.0824 |
0.0545 |
|
40 |
0.3380 |
0.2626 |
0.2124 |
0.1819 |
0.1665 |
0.1478 |
0.1393 |
0.1299 |
0.1204 |
0.1059 |
0.0832 |
0.0639 |
0.0417 |
|
60 |
0.2617 |
0.1951 |
0.1588 |
0.1370 |
0.1197 |
0.1091 |
0.0997 |
0.0933 |
0.0867 |
0.0835 |
0.0640 |
0.0447 |
0.0285 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 15. Верхние процентные (5%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 3
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9986 |
0.9715 |
0.9294 |
0.8878 |
0.8604 |
0.8314 |
0.8031 |
0.7892 |
0.7696 |
0.7591 |
0.7051 |
0.6352 |
0.5684 |
|
3 |
0.9642 |
0.8500 |
0.7662 |
0.7131 |
0.6623 |
0.6377 |
0.6118 |
0.5946 |
0.5808 |
0.5630 |
0.5122 |
0.4506 |
0.3925 |
|
4 |
0.8980 |
0.7399 |
0.6486 |
0.5870 |
0.5499 |
0.5134 |
0.4617 |
0.4811 |
0.4646 |
0.4543 |
0.4060 |
0.3526 |
0.2996 |
|
5 |
0.8359 |
0.6524 |
0.5487 |
0.4972 |
0.4663 |
0.4383 |
0.4196 |
0.3994 |
0.3882 |
0.3759 |
0.3379 |
0.2897 |
0.2422 |
|
6 |
0.7643 |
0.5751 |
0.4845 |
0.4400 |
0.4029 |
0.3803 |
0.3611 |
0.3473 |
0.3311 |
0.3282 |
0.2876 |
0.2452 |
0.2037 |
|
7 |
0.6979 |
0.5209 |
0.4351 |
0.3894 |
0.3563 |
0.3353 |
0.3160 |
0.3051 |
0.2965 |
0.2843 |
0.2529 |
0.2131 |
0.1763 |
|
8 |
0.6461 |
0.4692 |
0.3895 |
0.3500 |
0.3227 |
0.2980 |
0.2856 |
0.2734 |
0.2634 |
0.2542 |
0.2240 |
0.1876 |
0.1550 |
|
9 |
0.6106 |
0.4309 |
0.3616 |
0.3169 |
0.2924 |
0.2725 |
0.2578 |
0.2469 |
0.2361 |
0.2308 |
0.2024 |
0.1691 |
0.1387 |
|
10 |
0.5556 |
0.3944 |
0.3334 |
0.2912 |
0.2686 |
0.2485 |
0.2342 |
0.2251 |
0.2188 |
0.2115 |
0.1832 |
0.1533 |
0.1255 |
|
12 |
0.5003 |
0.3510 |
0.2846 |
0.2519 |
0.2291 |
0.2126 |
0.2005 |
0.1930 |
0.1837 |
0.1797 |
0.1558 |
0.1296 |
0.1055 |
|
15 |
0.4286 |
0.2947 |
0.2382 |
0.2069 |
0.1897 |
0.1760 |
0.1658 |
0.1588 |
0.1529 |
0.1467 |
0.1272 |
0.1057 |
0.0850 |
|
20 |
0.3464 |
0.2317 |
0.1900 |
0.1630 |
0.1463 |
0.1385 |
0.1284 |
0.1223 |
0.1178 |
0.1131 |
0.0978 |
0.0808 |
0.0643 |
|
24 |
0.3019 |
0.1983 |
0.1632 |
0.1402 |
0.1260 |
0.1161 |
0.1102 |
0.1036 |
0.0997 |
0.0967 |
0.0832 |
0.0677 |
0.0540 |
|
30 |
0.2556 |
0.1647 |
0.1325 |
0.1151 |
0.1029 |
0.0966 |
0.0890 |
0.0858 |
0.0823 |
0.0785 |
0.0678 |
0.0550 |
0.0434 |
|
40 |
0.2034 |
0.1304 |
0.1044 |
0.0886 |
0.0808 |
0.0736 |
0.0689 |
0.0663 |
0.0633 |
0.0608 |
0.0520 |
0.0419 |
0.0329 |
|
60 |
0.1447 |
0.0920 |
0.0724 |
0.0621 |
0.0552 |
0.0514 |
0.0482 |
0.0459 |
0.0434 |
0.0417 |
0.0357 |
0.0285 |
0.0221 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 16. Верхние процентные (5%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 5
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9986 |
0.9672 |
0.9189 |
0.8837 |
0.8366 |
0.8115 |
0.7882 |
0.7668 |
0.7467 |
0.7407 |
0.6867 |
0.6202 |
0.5595 |
|
3 |
0.9656 |
0.8437 |
0.7518 |
0.6921 |
0.6456 |
0.6130 |
0.5904 |
0.5657 |
0.5538 |
0.5428 |
0.4913 |
0.4364 |
0.3847 |
|
4 |
0.8962 |
0.7216 |
0.6218 |
0.5636 |
0.5108 |
0.4874 |
0.4687 |
0.4485 |
0.4383 |
0.4280 |
0.3854 |
0.3381 |
0.2927 |
|
5 |
0.8211 |
0.6189 |
0.5229 |
0.4749 |
0.4357 |
0.4096 |
0.3931 |
0.3760 |
0.3654 |
0.3547 |
0.3183 |
0.2776 |
0.2364 |
|
6 |
0.7587 |
0.5465 |
0.4604 |
0.4085 |
0.3696 |
0.3508 |
0.3356 |
0.3196 |
0.3110 |
0.3015 |
0.2699 |
0.2345 |
0.1985 |
|
7 |
0.6969 |
0.4900 |
0.4065 |
0.3605 |
0.3285 |
0.3079 |
0.2957 |
0.2835 |
0.2715 |
0.2626 |
0.2372 |
0.2033 |
0.1716 |
|
8 |
0.6263 |
0.4441 |
0.3619 |
0.3197 |
0.2957 |
0.2761 |
0.2614 |
0.2513 |
0.2413 |
0.2353 |
0.2094 |
0.1786 |
0.1509 |
|
9 |
0.5815 |
0.3995 |
0.3309 |
0.2911 |
0.2638 |
0.2507 |
0.2367 |
0.2266 |
0.2178 |
0.2117 |
0.1886 |
0.1609 |
0.1347 |
|
10 |
0.5488 |
0.3633 |
0.3004 |
0.2644 |
0.2420 |
0.2261 |
0.2171 |
0.2058 |
0.1996 |
0.1922 |
0.1704 |
0.1454 |
0.1219 |
|
12 |
0.4735 |
0.3180 |
0.2565 |
0.2276 |
0.2065 |
0.1935 |
0.1828 |
0.1756 |
0.1680 |
0.1645 |
0.1449 |
0.1225 |
0.1021 |
|
15 |
0.4046 |
0.2644 |
0.2118 |
0.1863 |
0.1702 |
0.1586 |
0.1507 |
0.1432 |
0.1388 |
0.1340 |
0.1176 |
0.0995 |
0.0822 |
|
20 |
0.3163 |
0.2048 |
0.1659 |
0.1440 |
0.1310 |
0.1231 |
0.1157 |
0.1103 |
0.1067 |
0.1022 |
0.0900 |
0.0757 |
0.0622 |
|
24 |
0.2739 |
0.1739 |
0.1418 |
0.1232 |
0.1114 |
0.1034 |
0.0992 |
0.0933 |
0.0899 |
0.0875 |
0.0761 |
0.0637 |
0.0521 |
|
30 |
0.2280 |
0.1423 |
0.1153 |
0.1008 |
0.0908 |
0.0849 |
0.0755 |
0.0766 |
0.0737 |
0.0709 |
0.0620 |
0.0515 |
0.0419 |
|
40 |
0.1779 |
0.1104 |
0.0898 |
0.0773 |
0.0706 |
0.0650 |
0.0610 |
0.0592 |
0.0563 |
0.0546 |
0.0476 |
0.0392 |
0.0317 |
|
60 |
0.1241 |
0.0765 |
0.0613 |
0.0536 |
0.0481 |
0.0450 |
0.0424 |
0.0404 |
0.0386 |
0.0372 |
0.0324 |
0.0265 |
0.0213 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 17. Верхние процентные (5%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 10
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9987 |
0.9678 |
0.9166 |
0.8752 |
0.8277 |
0.7996 |
0.7784 |
0.7530 |
0.7337 |
0.7259 |
0.6718 |
0.6097 |
0.5547 |
|
3 |
0.9664 |
0.8423 |
0.7380 |
0.6795 |
0.6323 |
0.5972 |
0.5762 |
0.5492 |
0.5364 |
0.5272 |
0.4793 |
0.4265 |
0.3798 |
|
4 |
0.8946 |
0.7097 |
0.6075 |
0.5436 |
0.4936 |
0.4684 |
0.4530 |
0.4313 |
0.4230 |
0.4124 |
0.3741 |
0.3293 |
0.2887 |
|
5 |
0.8175 |
0.5997 |
0.5051 |
0.4529 |
0.4152 |
0.3918 |
0.3771 |
0.3613 |
0.3514 |
0.3403 |
0.3073 |
0.2691 |
0.2330 |
|
6 |
0.7527 |
0.5301 |
0.4403 |
0.3887 |
0.3532 |
0.3356 |
0.3211 |
0.3040 |
0.2982 |
0.2890 |
0.2603 |
0.2278 |
0.1956 |
|
7 |
0.6855 |
0.4706 |
0.3867 |
0.3416 |
0.3117 |
0.2916 |
0.2796 |
0.2694 |
0.2590 |
0.2502 |
0.2276 |
0.1972 |
0.1688 |
|
8 |
0.6164 |
0.4249 |
0.3431 |
0.3009 |
0.2792 |
0.2612 |
0.2468 |
0.2380 |
0.2292 |
0.2235 |
0.2010 |
0.1731 |
0.1484 |
|
9 |
0.5697 |
0.3790 |
0.3119 |
0.2741 |
0.2490 |
0.2365 |
0.2256 |
0.2152 |
0.2071 |
0.2012 |
0.1804 |
0.1559 |
0.1325 |
|
10 |
0.5352 |
0.3428 |
0.2828 |
0.2497 |
0.2276 |
0.2129 |
0.2053 |
0.1944 |
0.1888 |
0.1821 |
0.1628 |
0.1410 |
0.1196 |
|
12 |
0.4616 |
0.2972 |
0.2394 |
0.2129 |
0.1934 |
0.1817 |
0.1720 |
0.1652 |
0.1600 |
0.1557 |
0.1379 |
0.1183 |
0.1002 |
|
15 |
0.3862 |
0.2462 |
0.1953 |
0.1737 |
0.1588 |
0.1480 |
0.1412 |
0.1344 |
0.1307 |
0.1266 |
0.1120 |
0.0960 |
0.0806 |
|
20 |
0.2993 |
0.1873 |
0.1527 |
0.1330 |
0.1219 |
0.1142 |
0.1086 |
0.1030 |
0.1001 |
0.0960 |
0.0855 |
0.0729 |
0.0610 |
|
24 |
0.2564 |
0.1569 |
0.1294 |
0.1136 |
0.1028 |
0.0962 |
0.0921 |
0.0872 |
0.0841 |
0.0818 |
0.0722 |
0.0612 |
0.0510 |
|
30 |
0.2108 |
0.1274 |
0.1052 |
0.0924 |
0.0837 |
0.0784 |
0.0739 |
0.0711 |
0.0687 |
0.0665 |
0.0586 |
0.0494 |
0.0410 |
|
40 |
0.1619 |
0.0978 |
0.0813 |
0.0701 |
0.0648 |
0.0597 |
0.0565 |
0.0546 |
0.0521 |
0.0509 |
0.0447 |
0.0375 |
0.0310 |
|
60 |
0.1103 |
0.0668 |
0.0549 |
0.0486 |
0.0439 |
0.0413 |
0.0391 |
0.0373 |
0.0358 |
0.0345 |
0.0305 |
0.0254 |
0.0208 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 18. Верхние процентные (10%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 0.5
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9984 |
0.9892 |
0.9794 |
0.9693 |
0.9596 |
0.9502 |
0.9402 |
0.9356 |
0.9278 |
0.9210 |
0.8864 |
0.8094 |
0.6860 |
|
3 |
0.9794 |
0.9479 |
0.9245 |
0.9026 |
0.8833 |
0.8641 |
0.8500 |
0.8382 |
0.8183 |
0.8085 |
0.7540 |
0.6558 |
0.5087 |
|
4 |
0.9499 |
0.9030 |
0.8642 |
0.8355 |
0.8139 |
0.7889 |
0.7682 |
0.7528 |
0.7343 |
0.7287 |
0.6619 |
0.5586 |
0.4068 |
|
5 |
0.9261 |
0.8653 |
0.8190 |
0.7769 |
0.7581 |
0.7331 |
0.7102 |
0.6974 |
0.6831 |
0.6661 |
0.6027 |
0.4853 |
0.3416 |
|
6 |
0.8914 |
0.8258 |
0.7698 |
0.7390 |
0.7146 |
0.6896 |
0.6618 |
0.6440 |
0.6333 |
0.6168 |
0.5450 |
0.4351 |
0.2907 |
|
7 |
0.8636 |
0.7871 |
0.7492 |
0.7092 |
0.6684 |
0.6504 |
0.6308 |
0.6069 |
0.5919 |
0.5790 |
0.5035 |
0.3843 |
0.2583 |
|
8 |
0.8424 |
0.7642 |
0.7025 |
0.6730 |
0.6481 |
0.6165 |
0.5950 |
0.5723 |
0.5576 |
0.5429 |
0.4655 |
0.3549 |
0.2303 |
|
9 |
0.8163 |
0.7402 |
0.6825 |
0.6478 |
0.6116 |
0.5828 |
0.5627 |
0.5442 |
0.5296 |
0.5084 |
0.4413 |
0.3271 |
0.2090 |
|
10 |
0.7912 |
0.7099 |
0.6654 |
0.6184 |
0.5884 |
0.5653 |
0.5404 |
0.5194 |
0.4960 |
0.4772 |
0.4106 |
0.3038 |
0.1914 |
|
12 |
0.7607 |
0.6721 |
0.6170 |
0.5688 |
0.5457 |
0.5143 |
0.4930 |
0.4738 |
0.4565 |
0.4402 |
0.3669 |
0.2633 |
0.1632 |
|
15 |
0.7184 |
0.6190 |
0.5624 |
0.5284 |
0.4887 |
0.4718 |
0.4405 |
0.4240 |
0.4054 |
0.3863 |
0.3166 |
0.2220 |
0.1342 |
|
20 |
0.6451 |
0.5517 |
0.5080 |
0.4634 |
0.4230 |
0.4095 |
0.3796 |
0.3586 |
0.3405 |
0.3273 |
0.2620 |
0.1772 |
0.1037 |
|
24 |
0.6069 |
0.5155 |
0.4694 |
0.4203 |
0.3945 |
0.3663 |
0.3478 |
0.3218 |
0.3036 |
0.2902 |
0.2288 |
0.1530 |
0.0884 |
|
30 |
0.5588 |
0.4685 |
0.4167 |
0.3759 |
0.3442 |
0.3200 |
0.2990 |
0.2797 |
0.2647 |
0.2483 |
0.1931 |
0.1271 |
0.0729 |
|
40 |
0.4862 |
0.4192 |
0.3573 |
0.3204 |
0.2942 |
0.2659 |
0.2448 |
0.2290 |
0.2142 |
0.2047 |
0.1537 |
0.1000 |
0.0564 |
|
60 |
0.4044 |
0.3369 |
0.2865 |
0.2495 |
0.2221 |
0.1969 |
0.1819 |
0.1692 |
0.1579 |
0.1477 |
0.1099 |
0.0711 |
0.0392 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 19. Верхние процентные (10%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 1 (распределению Лапласа)
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9959 |
0.9685 |
0.9418 |
0.9172 |
0.8943 |
0.8744 |
0.8567 |
0.8488 |
0.8321 |
0.8228 |
0.7755 |
0.6978 |
0.6062 |
|
3 |
0.9545 |
0.8793 |
0.8260 |
0.7877 |
0.7556 |
0.7295 |
0.7114 |
0.6883 |
0.6722 |
0.6612 |
0.5971 |
0.5185 |
0.4282 |
|
4 |
0.8952 |
0.7956 |
0.7401 |
0.6913 |
0.6532 |
0.6243 |
0.6054 |
0.5808 |
0.5720 |
0.5553 |
0.4962 |
0.4196 |
0.3321 |
|
5 |
0.8418 |
0.7200 |
0.6572 |
0.6145 |
0.5859 |
0.5523 |
0.5335 |
0.5107 |
0.4994 |
0.4828 |
0.4277 |
0.3510 |
0.2729 |
|
6 |
0.7897 |
0.6705 |
0.6035 |
0.5541 |
0.5175 |
0.4948 |
0.4794 |
0.4482 |
0.4388 |
0.4241 |
0.3749 |
0.3047 |
0.2309 |
|
7 |
0.7426 |
0.6209 |
0.5589 |
0.5086 |
0.4741 |
0.4547 |
0.4315 |
0.4100 |
0.3943 |
0.3807 |
0.3343 |
0.2666 |
0.2020 |
|
8 |
0.6981 |
0.5745 |
0.5166 |
0.4719 |
0.4399 |
0.4145 |
0.3894 |
0.3737 |
0.3639 |
0.3546 |
0.3019 |
0.2384 |
0.1784 |
|
9 |
0.6694 |
0.5467 |
0.4852 |
0.4413 |
0.4074 |
0.3843 |
0.3680 |
0.3517 |
0.3325 |
0.3202 |
0.2778 |
0.2169 |
0.1602 |
|
10 |
0.6366 |
0.5223 |
0.4567 |
0.4122 |
0.3790 |
0.3579 |
0.3410 |
0.3250 |
0.3111 |
0.2981 |
0.2547 |
0.1996 |
0.1460 |
|
12 |
0.5846 |
0.4683 |
0.4076 |
0.3673 |
0.3428 |
0.3163 |
0.2986 |
0.2856 |
0.2743 |
0.2645 |
0.2219 |
0.1704 |
0.1232 |
|
15 |
0.5220 |
0.4120 |
0.3549 |
0.3208 |
0.2947 |
0.2740 |
0.2545 |
0.2436 |
0.2365 |
0.2203 |
0.1857 |
0.1412 |
0.1004 |
|
20 |
0.4463 |
0.3470 |
0.2980 |
0.2649 |
0.2365 |
0.2264 |
0.2085 |
0.1989 |
0.1871 |
0.1800 |
0.1480 |
0.1102 |
0.0766 |
|
24 |
0.4032 |
0.3089 |
0.2662 |
0.2323 |
0.2137 |
0.1950 |
0.1842 |
0.1709 |
0.1634 |
0.1561 |
0.1283 |
0.0940 |
0.0647 |
|
30 |
0.3512 |
0.2699 |
0.2272 |
0.2001 |
0.1810 |
0.1668 |
0.1523 |
0.1465 |
0.1386 |
0.1303 |
0.1061 |
0.0770 |
0.0527 |
|
40 |
0.2970 |
0.2258 |
0.1862 |
0.1624 |
0.1480 |
0.1319 |
0.1233 |
0.1179 |
0.1085 |
0.1170 |
0.0905 |
0.0599 |
0.0402 |
|
60 |
0.2300 |
0.1727 |
0.1396 |
0.1211 |
0.1069 |
0.0964 |
0.0897 |
0.0847 |
0.0791 |
0.0758 |
0.0590 |
0.0417 |
0.0275 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 20. Верхние процентные (10%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 3
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9939 |
0.9440 |
0.8883 |
0.8441 |
0.8106 |
0.7862 |
0.7596 |
0.7481 |
0.8119 |
0.7191 |
0.6731 |
0.6156 |
0.5585 |
|
3 |
0.9286 |
0.7962 |
0.7104 |
0.6646 |
0.6180 |
0.5966 |
0.5752 |
0.5580 |
0.5445 |
0.5336 |
0.4865 |
0.4349 |
0.3844 |
|
4 |
0.8411 |
0.6757 |
0.5911 |
0.5402 |
0.5060 |
0.4789 |
0.4998 |
0.4491 |
0.4353 |
0.4255 |
0.3864 |
0.3384 |
0.2929 |
|
5 |
0.7698 |
0.5919 |
0.5007 |
0.4560 |
0.4298 |
0.4057 |
0.3891 |
0.3769 |
0.3643 |
0.3523 |
0.3195 |
0.2782 |
0.2376 |
|
6 |
0.7003 |
0.5245 |
0.4420 |
0.4045 |
0.3721 |
0.3549 |
0.3357 |
0.3239 |
0.3130 |
0.3049 |
0.2736 |
0.2351 |
0.1994 |
|
7 |
0.6340 |
0.4699 |
0.3986 |
0.3586 |
0.3304 |
0.3108 |
0.2938 |
0.2852 |
0.2780 |
0.2670 |
0.2400 |
0.2050 |
0.1728 |
|
8 |
0.5861 |
0.4273 |
0.3582 |
0.3218 |
0.2977 |
0.2777 |
0.2650 |
0.2557 |
0.2470 |
0.2394 |
0.2130 |
0.1801 |
0.1518 |
|
9 |
0.5544 |
0.3928 |
0.3316 |
0.2923 |
0.2689 |
0.2526 |
0.2395 |
0.2305 |
0.2222 |
0.2159 |
0.1914 |
0.1628 |
0.1358 |
|
10 |
0.5051 |
0.3597 |
0.3023 |
0.2686 |
0.2484 |
0.2318 |
0.2192 |
0.2103 |
0.2053 |
0.1979 |
0.1737 |
0.1471 |
0.1228 |
|
12 |
0.4481 |
0.3173 |
0.2606 |
0.2314 |
0.2128 |
0.1984 |
0.1883 |
0.1809 |
0.1738 |
0.1692 |
0.1487 |
0.1246 |
0.1030 |
|
15 |
0.3851 |
0.2660 |
0.2180 |
0.1931 |
0.1759 |
0.1643 |
0.1556 |
0.1485 |
0.1441 |
0.1380 |
0.1212 |
0.1017 |
0.0832 |
|
20 |
0.3139 |
0.2131 |
0.1733 |
0.1506 |
0.1369 |
0.1293 |
0.1208 |
0.1151 |
0.1112 |
0.1070 |
0.0934 |
0.0776 |
0.0630 |
|
24 |
0.2740 |
0.1809 |
0.1480 |
0.1300 |
0.1178 |
0.1091 |
0.1031 |
0.0979 |
0.0944 |
0.0913 |
0.0791 |
0.0654 |
0.0529 |
|
30 |
0.2303 |
0.1518 |
0.1227 |
0.1072 |
0.0964 |
0.0898 |
0.0839 |
0.0804 |
0.0777 |
0.0744 |
0.0645 |
0.0531 |
0.0426 |
|
40 |
0.1834 |
0.1192 |
0.0965 |
0.0828 |
0.0756 |
0.0691 |
0.0653 |
0.0625 |
0.0594 |
0.0574 |
0.0496 |
0.0405 |
0.0322 |
|
60 |
0.1317 |
0.0850 |
0.0674 |
0.0580 |
0.0519 |
0.0483 |
0.0457 |
0.0432 |
0.0412 |
0.0396 |
0.0341 |
0.0276 |
0.0217 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 21. Верхние процентные (10%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 5
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9940 |
0.9409 |
0.8787 |
0.8383 |
0.7906 |
0.7631 |
0.7429 |
0.7262 |
0.7104 |
0.7016 |
0.6546 |
0.6011 |
0.5509 |
|
3 |
0.9262 |
0.7862 |
0.6927 |
0.6435 |
0.6046 |
0.5711 |
0.5561 |
0.5324 |
0.5215 |
0.5135 |
0.4690 |
0.4214 |
0.3780 |
|
4 |
0.8410 |
0.6557 |
0.5750 |
0.5186 |
0.4771 |
0.4537 |
0.4386 |
0.4211 |
0.4115 |
0.4039 |
0.3691 |
0.3267 |
0.2871 |
|
5 |
0.7530 |
0.5597 |
0.4810 |
0.4350 |
0.4053 |
0.3808 |
0.3667 |
0.3525 |
0.3450 |
0.3342 |
0.3038 |
0.2665 |
0.2323 |
|
6 |
0.6821 |
0.4973 |
0.4243 |
0.3766 |
0.3460 |
0.3292 |
0.3137 |
0.3010 |
0.2947 |
0.2840 |
0.2582 |
0.2260 |
0.1950 |
|
7 |
0.6229 |
0.4441 |
0.3727 |
0.3308 |
0.3064 |
0.2888 |
0.2759 |
0.2671 |
0.2562 |
0.2486 |
0.2262 |
0.1964 |
0.1685 |
|
8 |
0.5616 |
0.4003 |
0.3326 |
0.2958 |
0.2730 |
0.2583 |
0.2440 |
0.2356 |
0.2289 |
0.2353 |
0.2094 |
0.1722 |
0.1480 |
|
9 |
0.5255 |
0.3626 |
0.3045 |
0.2709 |
0.2466 |
0.2336 |
0.2231 |
0.2139 |
0.2063 |
0.2008 |
0.1795 |
0.1557 |
0.1323 |
|
10 |
0.4922 |
0.3331 |
0.2775 |
0.2461 |
0.2258 |
0.2127 |
0.2039 |
0.1940 |
0.1891 |
0.1822 |
0.1632 |
0.1406 |
0.1196 |
|
12 |
0.4269 |
0.2900 |
0.2364 |
0.2119 |
0.1937 |
0.1816 |
0.1727 |
0.1659 |
0.1602 |
0.1558 |
0.1387 |
0.1185 |
0.1001 |
|
15 |
0.3641 |
0.2417 |
0.1961 |
0.1751 |
0.1591 |
0.1491 |
0.1414 |
0.1359 |
0.1317 |
0.1272 |
0.1128 |
0.0962 |
0.0808 |
|
20 |
0.2897 |
0.1896 |
0.1537 |
0.1347 |
0.1240 |
0.1161 |
0.1092 |
0.1047 |
0.1013 |
0.0975 |
0.0865 |
0.0733 |
0.0611 |
|
24 |
0.2500 |
0.1600 |
0.1313 |
0.1154 |
0.1047 |
0.0977 |
0.0929 |
0.0886 |
0.0858 |
0.0830 |
0.0731 |
0.0617 |
0.0512 |
|
30 |
0.2081 |
0.1324 |
0.1075 |
0.0945 |
0.0856 |
0.0802 |
0.0755 |
0.0723 |
0.0703 |
0.0678 |
0.0594 |
0.0500 |
0.0412 |
|
40 |
0.1635 |
0.1027 |
0.0836 |
0.0728 |
0.0667 |
0.0617 |
0.0582 |
0.0560 |
0.0536 |
0.0519 |
0.0455 |
0.0380 |
0.0311 |
|
60 |
0.1147 |
0.0721 |
0.0574 |
0.0504 |
0.0455 |
0.0427 |
0.0405 |
0.0384 |
0.0369 |
0.0356 |
0.0312 |
0.0258 |
0.0210 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 22. Верхние процентные (10%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению экспоненциального семейства с параметром формы 10
|
m\v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
|
2 |
0.9942 |
0.9402 |
0.8742 |
0.8280 |
0.7819 |
0.7532 |
0.7292 |
0.7152 |
0.6994 |
0.6901 |
0.6437 |
0.5928 |
0.5462 |
|
3 |
0.9276 |
0.7819 |
0.6834 |
0.6291 |
0.5892 |
0.5566 |
0.5408 |
0.5191 |
0.5069 |
0.5006 |
0.4578 |
0.4140 |
0.3736 |
|
4 |
0.8415 |
0.6453 |
0.5583 |
0.5030 |
0.4623 |
0.4381 |
0.4224 |
0.4071 |
0.3965 |
0.3901 |
0.3583 |
0.3190 |
0.2835 |
|
5 |
0.7464 |
0.5455 |
0.4642 |
0.4208 |
0.3876 |
0.3653 |
0.3527 |
0.3398 |
0.3317 |
0.3227 |
0.2942 |
0.2601 |
0.2293 |
|
6 |
0.6743 |
0.4819 |
0.4071 |
0.3596 |
0.3305 |
0.3146 |
0.3004 |
0.2886 |
0.2829 |
0.2741 |
0.2498 |
0.2206 |
0.1924 |
|
7 |
0.6174 |
0.4286 |
0.3542 |
0.3169 |
0.2923 |
0.2755 |
0.2640 |
0.2555 |
0.2456 |
0.2387 |
0.2177 |
0.1909 |
0.1660 |
|
8 |
0.5530 |
0.3825 |
0.3156 |
0.2817 |
0.2599 |
0.2448 |
0.2328 |
0.2251 |
0.2185 |
0.2137 |
0.1929 |
0.1680 |
0.1457 |
|
9 |
0.5130 |
0.3491 |
0.2878 |
0.2563 |
0.2341 |
0.2215 |
0.2113 |
0.2037 |
0.1976 |
0.1914 |
0.1722 |
0.1513 |
0.1303 |
|
10 |
0.4815 |
0.3162 |
0.2616 |
0.2326 |
0.2140 |
0.2020 |
0.1935 |
0.1849 |
0.1796 |
0.1731 |
0.1566 |
0.1365 |
0.1176 |
|
12 |
0.4165 |
0.2746 |
0.2219 |
0.1989 |
0.1822 |
0.1715 |
0.1634 |
0.1575 |
0.1522 |
0.1482 |
0.1325 |
0.1148 |
0.0984 |
|
15 |
0.3498 |
0.2248 |
0.1831 |
0.1643 |
0.1496 |
0.1401 |
0.1336 |
0.1284 |
0.1246 |
0.1204 |
0.1076 |
0.0930 |
0.0793 |
|
20 |
0.2733 |
0.1747 |
0.1426 |
0.1255 |
0.1156 |
0.1082 |
0.1025 |
0.0984 |
0.0956 |
0.0920 |
0.0825 |
0.0709 |
0.0600 |
|
24 |
0.2343 |
0.1466 |
0.1209 |
0.1067 |
0.0975 |
0.0916 |
0.0871 |
0.0833 |
0.0805 |
0.0782 |
0.0695 |
0.0596 |
0.0503 |
|
30 |
0.1948 |
0.1201 |
0.0984 |
0.0875 |
0.0794 |
0.0744 |
0.0706 |
0.0678 |
0.0658 |
0.0636 |
0.0564 |
0.0482 |
0.0404 |
|
40 |
0.1502 |
0.0918 |
0.0760 |
0.0671 |
0.0615 |
0.0573 |
0.0542 |
0.0521 |
0.0501 |
0.0488 |
0.0431 |
0.0365 |
0.0305 |
|
60 |
0.1032 |
0.0635 |
0.0520 |
0.0463 |
0.0419 |
0.0393 |
0.0375 |
0.0356 |
0.0344 |
0.0332 |
0.0296 |
0.0248 |
0.0205 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 23. Верхние процентные (1%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению нормальному закону [2]
|
m\n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
¥ |
|
2 |
0.9999 |
0.9950 |
0.9794 |
0.9586 |
0.9373 |
0.9172 |
0.8988 |
0.8823 |
0.8674 |
0.8539 |
0.7949 |
0.7067 |
0.6062 |
0.5000 |
|
3 |
0.9933 |
0.9423 |
0.8831 |
0.8335 |
0.7933 |
0.7606 |
0.7335 |
0.7107 |
0.6912 |
0.6743 |
0.6059 |
0.5153 |
0.4230 |
0.3333 |
|
4 |
0.9676 |
0.8643 |
0.7814 |
0.7212 |
0.6761 |
0.6410 |
0.6129 |
0.5897 |
0.5702 |
0.5536 |
0.4884 |
0.4057 |
0.3251 |
0.2500 |
|
5 |
0.9279 |
0.7885 |
0.6957 |
0.6329 |
0.5875 |
0.5531 |
0.5259 |
0.5037 |
0.4854 |
0.4697 |
0.4094 |
0.3351 |
0.2644 |
0.2000 |
|
6 |
0.8828 |
0.7218 |
0.6258 |
0.5653 |
0.5195 |
0.4866 |
0.4608 |
0.4401 |
0.4229 |
0.4084 |
0.3529 |
0.2858 |
0.2229 |
0.1667 |
|
7 |
0.8376 |
0.6644 |
0.5685 |
0.5080 |
0.4659 |
0.4347 |
0.4105 |
0.3911 |
0.6751 |
0.3616 |
0.3105 |
0.2494 |
0.1929 |
0.1429 |
|
8 |
0.7945 |
0.6152 |
0.5209 |
0.4927 |
0.4226 |
0.3932 |
0.3704 |
0.3522 |
0.3373 |
0.3248 |
0.2779 |
0.2214 |
0.1700 |
0.1250 |
|
9 |
0.7544 |
0.5727 |
0.4810 |
0.4251 |
0.3870 |
0.3592 |
0.3378 |
0.3207 |
0.3067 |
0.2950 |
0.2514 |
0.1992 |
0.1521 |
0.1111 |
|
10 |
0.7175 |
0.5358 |
0.4469 |
0.3934 |
0.3572 |
0.3308 |
0.3106 |
0.2945 |
0.2813 |
0.2704 |
0.2297 |
0.1811 |
0.1379 |
0.1000 |
|
12 |
0.6528 |
0.4751 |
0.3919 |
0.3428 |
0.3099 |
0.2861 |
0.2680 |
0.2535 |
0.2419 |
0.2320 |
0.1961 |
0.1535 |
0.1157 |
0.0833 |
|
15 |
0.5747 |
0.4069 |
0.3317 |
0.2882 |
0.2593 |
0.2386 |
0.2228 |
0.2104 |
0.2002 |
0.1918 |
0.1612 |
0.1251 |
0.0934 |
0.0667 |
|
20 |
0.4799 |
0.3297 |
0.2654 |
0.2288 |
0.2048 |
0.1877 |
0.1748 |
0.1646 |
0.1567 |
0.1501 |
0.1248 |
0.0960 |
0.0709 |
0.0500 |
|
24 |
0.4247 |
0.2871 |
0.2295 |
0.1970 |
0.1759 |
0.1608 |
0.1495 |
0.1406 |
0.1338 |
0.1283 |
0.1060 |
0.0810 |
0.0595 |
0.0417 |
|
30 |
0.3632 |
0.2412 |
0.1913 |
0.1635 |
0.1454 |
0.1327 |
0.1232 |
0.1157 |
0.1100 |
0.1054 |
0.0867 |
0.0658 |
0.0480 |
0.0333 |
|
40 |
0.2940 |
0.1915 |
0.1508 |
0.1281 |
0.1135 |
0.1033 |
0.0957 |
0.0898 |
0.0853 |
0.0816 |
0.0668 |
0.0503 |
0.0363 |
0.0250 |
|
60 |
0.2151 |
0.1371 |
0.1069 |
0.0902 |
0.0796 |
0.0722 |
0.0668 |
0.0625 |
0.0594 |
0.0567 |
0.0461 |
0.0344 |
0.0245 |
0.0167 |
|
120 |
0.1225 |
0.0759 |
0.0585 |
0.0489 |
0.0429 |
0.0387 |
0.0357 |
0.0334 |
0.0316 |
0.0302 |
0.0242 |
0.0178 |
0.0125 |
0.0083 |
|
¥ |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
Приложение 24. Верхние процентные (5%) точки для статистики (7) критерия Кохрена, построенной по m независимым оценкам дисперсии, каждая из которых обладает n степенями свободы. Выборка принадлежит распределению нормальному закону [2]
|
m\n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
¥ |
|
2 |
0.9985 |
0.9750 |
0.9392 |
0.9057 |
0.8772 |
0.8534 |
0.8332 |
0.8159 |
0.8010 |
0.7880 |
0.7341 |
0.6602 |
0.5812 |
0.5000 |
|
3 |
0.9669 |
0.8709 |
0.7977 |
0.7457 |
0.7071 |
0.6771 |
0.6530 |
0.6333 |
0.6167 |
0.6025 |
0.5466 |
0.4748 |
0.4031 |
0.3333 |
|
4 |
0.9065 |
0.7679 |
0.6841 |
0.6287 |
0.5895 |
0.5598 |
0.5365 |
0.5175 |
0.5017 |
0.4884 |
0.4366 |
0.3720 |
0.3093 |
0.2500 |
|
5 |
0.8412 |
0.6838 |
0.5981 |
0.5440 |
0.5063 |
0.4783 |
0.4564 |
0.4387 |
0.4241 |
0.4118 |
0.3645 |
0.3066 |
0.2513 |
0.2000 |
|
6 |
0.7808 |
0.6161 |
0.5321 |
0.4803 |
0.4447 |
0.4184 |
0.3980 |
0.3817 |
0.3682 |
0.3568 |
0.3135 |
0.2612 |
0.2119 |
0.1667 |
|
7 |
0.7271 |
0.5612 |
0.4800 |
0.4307 |
0.3974 |
0.3729 |
0.3535 |
0.3384 |
0.3259 |
0.3154 |
0.2756 |
0.2278 |
0.1833 |
0.1429 |
|
8 |
0.6798 |
0.5157 |
0.4377 |
0.3910 |
0.3595 |
0.3362 |
0.3185 |
0.3043 |
0.2926 |
0.2829 |
0.2462 |
0.2022 |
0.1616 |
0.1250 |
|
9 |
0.6385 |
0.4775 |
0.4027 |
0.3584 |
0.3286 |
0.3067 |
0.2901 |
0.2768 |
0.2659 |
0.2568 |
0.2226 |
0.1820 |
0.1446 |
0.1111 |
|
10 |
0.6020 |
0.4450 |
0.3733 |
0.3311 |
0.3029 |
0.2823 |
0.2666 |
0.2541 |
0.2439 |
0.2353 |
0.2032 |
0.1655 |
0.1308 |
0.1000 |
|
12 |
0.5410 |
0.3924 |
0.3264 |
0.2880 |
0.2624 |
0.2439 |
0.2299 |
0.2187 |
0.2098 |
0.2020 |
0.1737 |
0.1403 |
0.1100 |
0.0833 |
|
15 |
0.4709 |
0.3346 |
0.2758 |
0.2419 |
0.2195 |
0.2034 |
0.1911 |
0.1815 |
0.1736 |
0.1671 |
0.1429 |
0.1144 |
0.0889 |
0.0667 |
|
20 |
0.3894 |
0.2705 |
0.2205 |
0.1921 |
0.1735 |
0.1602 |
0.1501 |
0.1422 |
0.1357 |
0.1303 |
0.1108 |
0.0879 |
0.0675 |
0.0500 |
|
24 |
0.3434 |
0.2354 |
0.1907 |
0.1656 |
0.1493 |
0.1374 |
0.1286 |
0.1216 |
0.1160 |
0.1113 |
0.0942 |
0.0743 |
0.0567 |
0.0417 |
|
30 |
0.2929 |
0.1980 |
0.1593 |
0.1377 |
0.1237 |
0.1137 |
0.1061 |
0.1002 |
0.0958 |
0.0921 |
0.0771 |
0.0604 |
0.0457 |
0.0333 |
|
40 |
0.2370 |
0.1576 |
0.1259 |
0.1082 |
0.0968 |
0.0887 |
0.0827 |
0.0780 |
0.0745 |
0.0713 |
0.0595 |
0.0462 |
0.0347 |
0.0250 |
|
60 |
0.1737 |
0.1131 |
0.0895 |
0.0765 |
0.0682 |
0.0623 |
0.0583 |
0.0552 |
0.0520 |
0.0497 |
0.0411 |
0.0316 |
0.0234 |
0.0167 |
|
120 |
0.0998 |
0.0632 |
0.0495 |
0.0419 |
0.0371 |
0.0337 |
0.0312 |
0.0292 |
0.0279 |
0.0266 |
0.0218 |
0.0165 |
0.0120 |
0.0083 |
|
¥ |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
Приложение 25. Процентные точки F-распределения. Q = 5%
|
n2 \ n1 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
20 |
3.0984 |
2.8661 |
2.7109 |
2.5990 |
2.5140 |
2.4471 |
2.3928 |
2.3479 |
|
21 |
3.0725 |
2.8401 |
2.6848 |
2.5727 |
2.4879 |
2.4205 |
2.3661 |
2.3210 |
|
22 |
3.0491 |
2.8167 |
2.6613 |
2.5491 |
2.4638 |
2.3965 |
2.3419 |
2.2967 |
|
23 |
3.0280 |
2.7955 |
2.6400 |
2.5277 |
2.4422 |
2.3748 |
2.3201 |
2.2747 |
|
24 |
3.0088 |
2.7763 |
2.6207 |
2.5082 |
2.4226 |
2.3551 |
2.3002 |
2.2547 |
|
25 |
2.9912 |
2.7587 |
2.6030 |
2.4904 |
2.4047 |
2.3371 |
2.2821 |
2.2365 |
|
26 |
2.9751 |
2.7426 |
2.5868 |
2.4741 |
2.3883 |
2.3205 |
2.2655 |
2.2197 |
|
27 |
2.9604 |
2.7278 |
2.5719 |
2.4591 |
2.3732 |
2.3053 |
2.2501 |
2.2043 |
|
28 |
2.9467 |
2.7141 |
2.5581 |
2.4453 |
2.3593 |
2.2913 |
2.2360 |
2.1900 |
|
29 |
2.9340 |
2.7014 |
2.5454 |
2.4324 |
2.3463 |
2.2782 |
2.2229 |
2.1768 |
|
30 |
2.9223 |
2.6896 |
2.5336 |
2.4205 |
2.3343 |
2.2662 |
2.2107 |
2.1646 |
|
40 |
2.8387 |
2.6060 |
2.4459 |
2.3359 |
2.2490 |
2.1802 |
2.1240 |
2.0772 |
|
60 |
2.7581 |
2.5252 |
2.3683 |
2.2540 |
2.1665 |
2.0970 |
2.0401 |
1.9926 |
|
120 |
2.6802 |
2.4472 |
2.2900 |
2.1750 |
2.0867 |
2.0164 |
1.9588 |
1.9105 |
|
∞ |
2.6049 |
2.3719 |
2.2141 |
2.0986 |
2.0096 |
1.9384 |
1.8799 |
1.8307 |