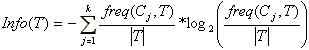2.1. Понятие информативности
Эвристическое определение
информативности Интуитивно предикат (φ тем более информативен, чем
больше он покрывает объектов некоторого фиксированного «своего» класса с
Y по
сравнению с объектами всех остальных «чужих» классов. Введём следующие
обозначения:
Gc — число объектов класса с в выборке Xе-]
gс(φ) — из них число объектов, для которых выполняется условие (φ(х) = 1);
Вс — число объектов всех остальных классов Y \ {с} в выборке Xl
bс(φ) — из них число объектов, для которых выполняется условие φ(х) = 1.
Для краткости индекс
с и аргумент (φ) будем
иногда опускать. Предполагается, что G
>= 1, В>= 1 и G + В =
l.
Чем больше
число покрываемых объектов (g + b)
и чем меньше среди них ошибочных b,
тем более информативен предикат φ. И, наоборот, наименее интересны предикаты, которые либо покрывают
слишком мало объектов, либо выделяют «свои» и «чужие» объекты примерно в той же
пропорции, в которой они представлены во всей выборке, b : g
~ В : G.
Введём обозначение Ес для доли ошибочно
покрываемых «чужих» объектов, и Dc
для доли всех покрываемых объектов:
Опр. Предикат φ(х) будем называть логической
закономерностью для класса с
Y,
если Ес(φ,Xl)
и Dc(φ,Xl)
при заданных
достаточно малом ε и достаточно большом δ из отрезка [0,1].
Если bс(φ) = 0, то закономерность φ называется чистой или непротиворечивой. Если bс(φ)> 0, то закономерность φ называется частичной.
В некоторых случаях имеет смысл ограничиваться поиском только чистых закономерностей. В частности, когда длина выборки мала или заранее известно, что данные практически не содержат шума. Такие прикладные задачи нередко встречаются на практике, например, классификация месторождений редких полезных ископаемых по данным геологоразведки.
Но чаще данные оказываются неполными и неточными. Таковы
многие медицинские и экономические задачи (в частности, задача о выдаче
кредитов). Для них незначительная доля ошибок ε на обучающей выборке
вполне допустима. Кроме того, существуют способы построения корректных
алгоритмов на основе частичных закономерностей, например, взвешенное
голосование. В этих случаях сравнивать и отбирать предикаты приходится по двум
критериям (g, b) одновременно. Что лучше: уменьшение
b на 1 или увеличение g на 10? Для
целенаправленного поиска лучших закономерностей удобнее иметь скалярный
критерий информативности.
Статистическое
определение информативности Адекватную скалярную характеристику
информативности даёт техника проверки статистических гипотез.
Пусть X
— вероятностное пространство, у*(х) и φ(х) — случайные величины.
Допустим, справедлива гипотеза о независимости событий {х: у*(х) = с} и {х:
(φ (х) = 1}. Тогда вероятность реализации пары (g,b) подчиняется гипергеометрическому распределению:
, где
Если вероятность мала, и тем не менее пара (g, b) реализовалась, то гипотеза о независимости, скорее всего, не верна. Тогда, возможно, между у* и φ имеется закономерная связь, и это тем возможнее, чем меньше значение вероятности.
Опр.
Информативность предиката φ(х) относительно класса с 
Y по выборке Xl есть
Предикат φ (х) будем называть статистической
закономерностью для класса с, если 
>I0
при заданном достаточно большом I0.
Порог
информативности I0 выбирается так, чтобы ему соответствовало достаточно
малое значение вероятности, называемое уровнем значимости. Например, при уровне
значимости 0.05 закономерностями являются предикаты с информативностью выше I0 = —ln
0.05 ~ 3.
Энтропийное определение информативности Ещё один способ определения информативности вытекает из теории информации.
Напомним, что если имеются два исхода w0, w1 с вероятностями р0 и p1 = 1 — р0 ,то количество информации, связанное с исходом wi по определению равно — log2pi. Энтропия определяется как мат.ожидание количества информации:
H(p0,
p1)=- p0*log2 p0- p1*log2
p1.
Если дана случайная независимая выборка, содержащая п0
исходов w0 и п0 исходов w1, то вероятности можно
оценить по выборке: 
и вычислить выборочную энтропию H(n0,n1) = H(p0,p1). Этих определений достаточно, чтобы
оценить информационный выигрыш, (information gain)
— количество информации об исходном делении выборки на два класса «с» и «не
с», которое содержится в предикате φ.
Исходная энтропия выборки Xl равна H(G, В).
Энтропия выборки после того, как стало известно, что предикат φ выделил g объектов из G и b объектов из В, есть
.
В итоге уменьшение энтропии (информационный выигрыш)
составляет IGainc(φ,
X1) = H(G, B) - H
φ(G, B, g, b}.
Согласно энтропийному критерию информативности предикат φ является закономерностью, если IGainc(φ, Xl )> G0 при некотором достаточно большом G0.
Теорема Энтропийный критерий IGainc асимптотически эквивалентен статистическому IС:
IGainc(φ, X1) 
при t 
.
2.2. Решающие деревья
Решающее дерево (decision tree, DT) — это логический алгоритм классификации, основанный на поиске конъюнктивных закономерностей.
Напомним некоторые понятия теории графов.
Деревом называется конечный связный граф с множеством
вершин V, не содержащий циклов и имеющий выделенную вершину 
, в которую не входит ни одно ребро. Эта вершина называется корнем дерева. Вершина, не
имеющая выходящих рёбер, называется терминальной
или листом. Остальные вершины называются внутренними.
Дерево называется бинарным, если из любой его внутренней вершины выходит ровно два ребра. Выходящие рёбра связывают внутреннюю вершину v с левой дочерней вершиной Lv и с правой дочерней вершиной Rv.
Опр. Бинарное решающее дерево — это алгоритм классификации, задающийся бинарным
деревом, в котором каждой внутренней вершине 
приписан предикат
, каждой терминальной вершине 
приписано имя класса cv 
Y. Правило классификации определяется следующим образом:
Алгоритм
:Классификация
объекта х 
X бинарным решающим деревом
1: v:=v0;
2: пока вершина v внутренняя
3: если
(x) то
4: v := Rv;
5: иначе
6: v := Lv-
7: вернуть cv.
2.3. Редукция решающих деревьев
Суть редукции состоит в удалении поддеревьев, имеющих недостаточную статистическую надёжность. При этом дерево перестаёт безошибочно классифицировать обучающую выборку, зато качество классификации новых объектов (способность к обобщению), как правило, улучшается.
Придумано огромное
количество эвристик для проведения редукции , однако ни одна из них, вообще говоря, не гарантирует улучшения
качества классификации.
Предредукция (pre-pruning)
или критерий раннего останова досрочно
прекращает дальнейшее ветвление в
вершине дерева, если информативность I(β, S) для всех
предикатов 
Β не дотягивает до заданного порогового значения I0.
Предредукция не является эффективным методом избежания переобучения, так как жадное ветвление по-прежнему остаётся глобально неоптимальным. Более эффективной считается стратегия постредукции.
Постредукция (post-pruning) просматривает все внутренние вершины дерева и заменяет отдельные вершины либо одной из дочерних вершин (при этом вторая дочерняя удаляется), либо терминальной вершиной. Процесс замен продолжается до тех пор, пока в дереве остаются вершины, удовлетворяющие критерию замены.
Критерием замены является сокращение числа ошибок на контрольной выборке, отобранной заранее и не участвовавшей в обучении дерева. Рекомендуется оставлять в контроле около 30% объектов. Наиболее экономичной реализацией постредукции является просмотр дерева методом поиска в глубину, при котором в каждой вершине дерева сохраняется информация о подмножестве контрольных объектов, попавших в данную вершину при классификации.
3. Описание алгоритмов построения деревьев решений
3.1. Алгоритм ID3
Идея алгоритма заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Проще всего записать этот алгоритм в виде рекурсивной процедуры LearnID3, которая строит дерево по заданной подвыборке S. Для построения полного дерева она применяется ко всей выборке и возвращает указатель на корень построенного дерева:
v0 := LearnID3 (Xl).
На шаге 6 алгоритма выбирается предикат β, задающий максимально информативное ветвление дерева — разбиение выборки на две части S = s0 U S1. На практике применяются различные критерии ветвления.
1. Критерий, ориентированный на скорейшее отделение одного из классов.
2. Критерий, ориентированный на задачи с большим числом классов. Фактически, это обобщение статистического определения информативности.
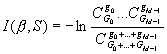,где
Gc-число объектов класса с в выборке S, из них gc объектов покрываются правилом β.
3. D-критерий — число пар объектов из
разных классов, на которых предикат β принимает разные значения. В случае
двух классов он имеет вид
I(β,S)=g(β)(B-b(β))+b(β)(G-g(β)).
Трудоёмкость алгоритма ID3 составляет O(|B|Vol), где v0 — число внутренних вершин дерева.
Алгоритм :Рекурсивный алгоритм построения решающего дерева ID3 Вход:
S — обучающая выборка;
В — множество базовых предикатов;
Выход:
Возвращает корневую вершину дерева, построенного по выборке S;
1: ПРОЦЕДУРА LearnID3 (S);
2:
если все объекты из S лежат в одном классе с 
Y то
3: создать новый лист v;
4: cv:=c;
5: вернуть (v);
6: найти предикат с максимальной информативностью:
β:= arg
;
7: разбить
выборку на две части S
= 
по предикату β: 
8: если 
или 
то
9: создать новый лист v;
10:cv := класс, в котором находится большинство объектов из
S;
11: вернуть (v);
12: иначе
13: создать новую внутреннюю вершину v;
14: βv:= β;
15: Lv := LearnID3 (So); (построить левое поддерево)
16: Rv := LearnID3 (S1); (построить правое поддерево)
17: вернуть (v);
Преимущества алгоритма ID3
-Простота и
интерпретируемость классификации. Алгоритм
способен
не только классифицировать объект, но и
выдать объяснение классификации
в терминах предметной области. Для этого достаточно записать
последователь
ность условий, пройденных объектом от корня дерева до листа.
-Алгоритм синтеза решающего дерева имеет сложность, линейную
по длине
выборки.
-Если множество
предикатов В настолько богато, что на шаге 6 всегда находится предикат, разбивающий выборку S на непустые подмножества s0 и S1,то алгоритм строит бинарное решающее
дерево, безошибочно классифицирую
щее выборку Xl.
-Алгоритм очень прост для
реализации и легко поддаётся различным усовершенствованиям. Можно использовать различные критерии ветвления и критерии
останова, вводить редукцию, и т. д.
Недостатки алгоритма ID3
-Жадность. Локально
оптимальный выбор предиката βV не является глобально
оптимальным. В случае выбора неоптимального предиката алгоритм не спосо
бен вернуться на уровень вверх и заменить неудачный предикат.
-Чем дальше вершина v расположена от корня дерева, тем меньше длина подвыборки S, по которой приходится принимать решение о
ветвлении в вершине v.
Тем менее статистически надёжным
является выбор предиката βV.
-Алгоритм склонен к переобучению — как правило, он переусложняет структуру дерева. Обобщающая способность алгоритма (качество классификации новыхобъектов) относительно невысока.
Основная причина недостатков — неоптимальность жадной стратегии наращивания дерева. Перечисленные недостатки в большей или меньшей степени свойственны большинству алгоритмов синтеза решающих деревьев. Для их устранения применяют различные эвристические приемы: редукцию, элементы глобальной оптимизации, «заглядывание вперёд» (look ahead).
3.2. Алгоритм CART
CART, сокращение от Classification And Regression Tree, переводится как 'Дерево Классификации и Регрессии' – алгоритм бинарного дерева решений, впервые опубликованный Бриманом и др. в 1984 году [1]. Алгоритм предназначен для решения задач классификации и регрессии. Существует также несколько модифицированных версий – алгоритмы IndCART и DB-CART. Алгоритм IndCART, является частью пакета Ind и отличается от CART использованием иного способа обработки пропущенных значений, не осуществляет регрессионную часть алгоритма CART и имеет иные параметры отсечения. Алгоритм DB-CART базируется на следующей идее: вместо того чтобы использовать обучающий набор данных для определения разбиений, используем его для оценки распределения входных и выходных значений и затем используем эту оценку, чтобы определить разбиения. DB, соответственно означает – 'distribution based'. Утверждается, что эта идея дает значительное уменьшение ошибки классификации, по сравнению со стандартными методами построения дерева. Основными отличиями алгоритма CART от алгоритмов семейства ID3 являются:
-бинарное представление дерева решений;
-функция оценки качества разбиения;
-механизм отсечения дерева;
-алгоритм обработки пропущенных значений;
-построение деревьев регрессии.
В алгоритме CART каждый узел дерева решений имеет двух потомков. На каждом шаге построения дерева правило, формируемое в узле, делит заданное множество примеров (обучающую выборку) на две части – часть, в которой выполняется правило (потомок – right) и часть, в которой правило не выполняется (потомок – left). Для выбора оптимального правила используется функция оценки качества разбиения.
Обучение дерева решений относится к классу обучения с учителем, то есть обучающая и тестовая выборки содержат классифицированный набор примеров. Оценочная функция, используемая алгоритмом CART, базируется на интуитивной идее уменьшения нечистоты (неопределённости) в узле. Рассмотрим задачу с двумя классами и узлом, имеющим по 50 примеров одного класса. Узел имеет максимальную 'нечистоту'. Если будет найдено разбиение, которое разбивает данные на две подгруппы 40:5 примеров в одной и 10:45 в другой, то интуитивно 'нечистота' уменьшится. Она полностью исчезнет, когда будет найдено разбиение, которое создаст подгруппы 50:0 и 0:50. В алгоритме CART идея 'нечистоты' формализована в индексе Gini. Если набор данных Т содержит данные n классов, тогда индекс Gini определяется как:
, где pi – вероятность (относительная частота) класса i в T.
Если набор Т разбивается на две части Т1 и Т2 с числом примеров в каждом N1 и N2 соответственно, тогда показатель качества разбиения будет равен:
Наилучшим считается то разбиение, для которого Ginisplit(T) минимально.
Обозначим N – число примеров в узле – предке, L, R – число примеров соответственно в левом и правом потомке, li и ri – число экземпляров i-го класса в левом/правом потомке. Тогда качество разбиения оценивается по следующей формуле:
Чтобы уменьшить объем вычислений формулу можно преобразовать:
Так как умножение на константу не играет роли при минимизации:
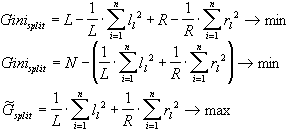
В итоге, лучшим будет то разбиение, для которого величина 
максимальна. Реже в алгоритме CART
используются другие критерии разбиения Twoing, Symmetric Gini и др.
Вектор предикторных переменных, подаваемый на вход дерева
может содержать как числовые (порядковые) так и категориальные переменные. В
любом случае в каждом узле разбиение идет только по одной переменной. Если переменная числового типа, то в узле
формируется правило вида xi
<= c. Где с – некоторый порог, который
чаще всего выбирается как среднее арифметическое двух соседних упорядоченных значений переменной xi обучающей выборки.
Если переменная категориального типа, то в узле формируется правило xi 
V(xi), где V(xi) – некоторое
непустое подмножество множества значений переменной xi в обучающей выборке. Следовательно, для n значений числового атрибута
алгоритм сравнивает n-1
разбиений, а для категориального (2n-1 – 1). На каждом шаге
построения дерева алгоритм последовательно сравнивает все возможные разбиения
для всех атрибутов и выбирает наилучший атрибут и наилучшее разбиение для него.
Механизм отсечения дерева, оригинальное название minimal cost-complexity tree pruning, – наиболее серьезное отличие алгоритма CART от других алгоритмов построения дерева. CART рассматривает отсечение как получение компромисса между двумя проблемами: получение дерева оптимального размера и получение точной оценки вероятности ошибочной классификации.
Основная проблема отсечения – большое количество всех возможных отсеченных поддеревьев для одного дерева. Более точно, если бинарное дерево имеет |T| – листов, тогда существует ~[1.5028369|T|] отсечённых поддеревьев. И если дерево имеет хотя бы 1000 листов, тогда число отсечённых поддеревьев становится просто огромным.
Базовая идея метода – не рассматривать все возможные поддеревья, ограничившись только 'лучшими представителями' согласно приведённой ниже оценке.
Обозначим |T| –
число листов дерева, R(T) –
ошибка классификации дерева, равная отношению числа неправильно
классифицированных примеров к числу примеров в обучающей выборке. Определим C
(T) –
полную стоимость (оценку/показатель затраты-сложность) дерева Т как:
C(T) =
R(T) + *|T|,
где |T| – число
листов (терминальных узлов) дерева, –
некоторый параметр, изменяющийся от 0 до +
. Полная
стоимость дерева состоит из двух компонент – ошибки классификации дерева и
штрафа за его сложность. Если ошибка классификации дерева неизменна, тогда с
увеличением полная
стоимость дерева будет увеличиваться. Тогда в зависимости от менее
ветвистое дерево, дающее бОльшую ошибку классификации может стоить меньше, чем
дающее меньшую ошибку, но более ветвистое.
Определим Tmax –
максимальное по размеру дерево, которое предстоит обрезать. Если мы зафиксируем
значение , тогда
существует наименьшее минимизируемое поддерево , которое
выполняет следующие условия:
С(T()) = minT
<= Tmax C(T)
if C
(T) = C
(T(
)) then T(
) <= T
Первое условие говорит, что не существует такого поддерева
дерева Tmax ,
которое имело бы меньшую стоимость, чем Т()
при этом значении . Второе
условие говорит, что если существует более одного поддерева, имеющего данную
полную стоимость, тогда мы выбираем наименьшее дерево.
Можно показать, что для любого значения 
существует
такое наименьшее минимизируемое поддерево. Но эта задача не тривиальна. Что она
говорит – что не может быть такого, когда два дерева достигают минимума
полной стоимости и они несравнимы, т.е. ни одно из них не является поддеревом
другого. Мы не будем доказывать этот результат.
Хотя 
имеет
бесконечное число значений, существует конечное число поддеревьев дерева Tmax.
Можно построить последовательность уменьшающихся поддеревьев дерева Tmax:
T1 > T2 > T3 > … > {t1}
,(где t1 – корневой узел дерева) такую, что Tk – наименьшее
минимизируемое поддерево для 
[
k,
k+1).
Это важный результат, так как это означает, что мы можем получить следующее
дерево в последовательности, применив отсечение к текущему дереву. Это
позволяет разработать эффективный алгоритм поиска наименьшего минимизируемого
поддерева при различных значениях . Первое
дерево в этой последовательности – наименьшее поддерево дерева Tmax, имеющее такую же
ошибку классификации, как и Tmax, т.е. T1 = T(
= 0).
Пояснение: если разбиение идет до тех пор, пока в каждом узле останется только
один класс, то T1 = Tmax, но так как часто применяются
методы ранней остановки (prepruning), тогда может существовать поддерево дерева
Tmax имеющее такую же ошибку классификации.
Как мы получаем
следующее дерево в последовательности и соответствующее значение 
? Обозначим Tt – ветвь дерева Т с корневым узлом t. При каких значениях 
дерево T – Tt будет лучше, чем Т?
Если мы отсечём в узле t,
тогда его вклад в полную стоимость дерева T – Tt станет C({t})
= R(t) + , где R(t) = r(t)* p(t), r(t) – это ошибка классификации узла t и p(t) – пропорция
случаев, которые 'прошли' через узел t. Альтернативный вариант: R(t)= m/n, где m – число примеров
классифицированных некорректно, а n –
общее число классифицируемых примеров для всего дерева.
Вклад Tt в полную стоимость дерева Т составит C(Tt)
= R(Tt) + |Tt|, где
Дерево T – Tt будет лучше, чем Т, когда C
({t}) = C
(Tt), потому что при этой величине они имеют
одинаковую стоимость, но T – Tt наименьшее из двух. Когда C({t}) = C(Tt) мы получаем:
решая для , получаем:
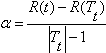
Так для любого узла
t в Т1 ,если мы увеличиваем , тогда
когда
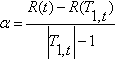
дерево, полученное
отсечением в узле t, будет лучше, чем Т1.
Основная идея состоит в следующем: вычислим это значение для каждого
узла в дереве Т1, и затем выберем 'слабые связи' (их может быть больше
чем одна), т.е. узлы для которых величина
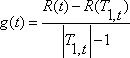
является наименьшей. Мы отсекаем Т1 в этих узлах, чтобы получить
Т2 – следующее дерево в последовательности. Затем мы продолжаем
этот процесс для полученного дерева и так пока мы не получим корневой узел
(дерево в котором только один узел).
3.3. Алгоритм С4.5
Прежде чем приступить к описанию алгоритма построения дерева решений, определим обязательные требования к структуре данных и непосредственно к самим данным, при выполнении которых алгоритм C4.5 будет работоспособен:
Описание атрибутов. Данные, необходимые для работы алгоритма, должны быть представлены в виде плоской таблицы. Вся информация об объектах (далее примеры) из предметной области должна описываться в виде конечного набора признаков (далее атрибуты). Каждый атрибут должен иметь дискретное или числовое значение. Сами атрибуты не должны меняться от примера к примеру, и количество атрибутов должно быть фиксированным для всех примеров.
Определенные классы. Каждый пример должен быть ассоциирован с конкретным классом, т.е. один из атрибутов должен быть выбран в качестве метки класса.
Дискретные классы. Классы должны быть дискретными, т.е. иметь конечное число значений. Каждый пример должен однозначно относиться к конкретному классу. Случаи, когда примеры принадлежат к классу с вероятностными оценками, исключаются. Количество классов должно быть значительно меньше количества примеров.
Пусть нам задано множество примеров T, где каждый элемент
этого множества описывается m атрибутами. Количество примеров в множестве T
будем называть мощностью этого множества и будем обозначать |T|.
Пусть метка класса принимает следующие значения C1, C2 …
Ck.
Наша задача будет заключаться в построении иерархической
классификационной модели в виде дерева из множества примеров T. Процесс
построения дерева будет происходить сверху вниз. Сначала создается корень
дерева, затем потомки корня и т.д.
На первом шаге мы имеем пустое дерево (имеется только корень) и исходное
множество T (ассоциированное с корнем). Требуется разбить исходное множество на
подмножества. Это можно сделать, выбрав один из атрибутов в качестве проверки.
Тогда в результате разбиения получаются n(по числу значений атрибута)
подмножеств и, сответственно, создаются n потомков корня, каждому из которых
поставлено в соответствие свое подмножество, полученное при разбиении множества
T. Затем эта процедура рекурсивно применяется ко всем подмножествам (потомкам
корня) и т.д.
Рассмотрим подробнее критерий выбора атрибута, по которому должно пойти ветвление. Очевидно, что в нашем распоряжении m (по числу атрибутов) возможных вариантов, из которых мы должны выбрать самый подходящий. Некоторые алгоритмы исключают повторное использование атрибута при построении дерева, но в нашем случае мы таких ограничений накладывать не будем. Любой из атрибутов можно использовать неограниченное количество раз при построении дерева.
Пусть мы имеем проверку X (в качестве проверки может быть выбран любой атрибут), которая принимает n значений A1, A2 … An. Тогда разбиение T по проверке X даст нам подмножества T1, T2 … Tn, при X равном соответственно A1, A2 … An. Единственная доступная нам информация – то, каким образом классы распределены в множестве T и его подмножествах, получаемых при разбиении по X. Именно этим мы и воспользуемся при определении критерия.
Пусть 
–
количество примеров из некоторого множества S, относящихся к одному и тому же
классу Cj. Тогда вероятность того, что случайно выбранный пример из
множества S будет принадлежать к классу Cj
|
|
|
Согласно теории информации, количество содержащейся в сообщении информации, зависит от ее вероятности
|
|
(1) |
Поскольку мы используем логарифм с двоичным основанием, то выражение (1) дает количественную оценку в битах.
Выражение
|
|
(2) |
дает оценку среднего количества информации, необходимого для определения класса примера из множества T. В терминологии теории информации выражение (2) называется энтропией множества T.
Ту же оценку, но только уже после разбиения множества T по X, дает следующее выражение:
|
|
(3) |
Тогда критерием для выбора атрибута будет являться следующая формула:
|
|
(4) |
Критерий (4) считается для всех атрибутов. Выбирается атрибут, максимизирующий данное выражение. Этот атрибут будет являться проверкой в текущем узле дерева, а затем по этому атрибуту производится дальнейшее построение дерева. Т.е. в узле будет проверяться значение по этому атрибуту и дальнейшее движение по дереву будет производиться в зависимости от полученного ответа.
Такие же рассуждения можно применить к полученным
подмножествам T1, T2 … Tn и продолжить
рекурсивно процесс построения дерева, до тех пор, пока в узле не окажутся
примеры из одного класса.
Одно важное замечание: если в процессе работы алгоритма получен узел, ассоциированный с пустым множеством (т.е. ни один пример не попал в данный узел), то он помечается как лист, и в качестве решения листа выбирается наиболее часто встречающийся класс у непосредственного предка данного листа.
Здесь следует пояснить почему критерий (4) должен максимизироваться. Из свойств энтропии нам известно, что максимально возможное значение энтропии достигается в том случае, когда все его сообщения равновероятны. В нашем случае, энтропия (3) достигает своего максимума когда частота появления классов в примерах множества T равновероятна. Нам же необходимо выбрать такой атрибут, чтобы при разбиении по нему один из классов имел наибольшую вероятность появления. Это возможно в том случае, когда энтропия (3) будет иметь минимальное значение и, соответственно, критерий (4) достигнет своего максимума.
Как быть в случае с числовыми атрибутами? Понятно, что следует выбрать некий порог, с которым должны сравниваться все значения атрибута. Пусть числовой атрибут имеет конечное число значений. Обозначим их {v1, v2 … vn}. Предварительно отсортируем все значения. Тогда любое значение, лежащее между vi и vi+1, делит все примеры на два множества: те, которые лежат слева от этого значения {v1, v2 … vi}, и те, что справа {vi+1, vi+2 … vn}. В качестве порога можно выбрать среднее между значениями vi и vi+1
|
|
|
Таким образом, мы существенно упростили задачу нахождения
порога, и привели к рассмотрению всего n-1 потенциальных пороговых значений TH1,
TH2 … THn-1.
Формулы (2), (3) и (4) последовательно применяются ко всем потенциальным
пороговым значениям и среди них выбирается то, которое дает максимальное
значение по критерию (4). Далее это значение сравнивается со значениями
критерия (4), подсчитанными для остальных атрибутов. Если выяснится, что среди
всех атрибутов данный числовой атрибут имеет максимальное значение по критерию
(4), то в качестве проверки выбирается именно он.
Следует отметить, что все числовые тесты являются бинарными, т.е. делят узел дерева на две ветви.
Итак, мы имеем дерево решений и хотим использовать его для распознавания нового объекта. Обход дерева решений начинается с корня дерева. На каждом внутреннем узле проверяется значение объекта Y по атрибуту, который соответствует проверке в данном узле, и, в зависимости от полученного ответа, находится соответствующее ветвление, и по этой дуге двигаемся к узлу, находящему на уровень ниже и т.д. Обход дерева заканчивается как только встретится узел решения, который и дает название класса объекта Y.
Заключение
Несмотря на обилие методов Data Mining, приоритет постепенно все более смещается в сторону логических алгоритмов поиска в данных if-then правил, конкретно деревьев решений. С их помощью решаются задачи прогнозирования, классификации, распознавания образов, сегментации БД, извлечения из данных “скрытых” знаний, интерпретации данных, установления ассоциаций в БД и др. Результаты таких алгоритмов эффективны и легко интерпретируются.
Вместе с тем, главной проблемой логических методов обнаружения закономерностей является проблема перебора вариантов за приемлемое время. Другие проблемы связаны с тем, что известные методы поиска логических правил не поддерживают функцию обобщения найденных правил и функцию поиска оптимальной композиции таких правил.
Список использованных источников
1. Материалы сайта InterfaceLtd.htm
2. Материалы сайта Лаборатория BaseGroup
3. К.В. Воронцов «Лекции по логическим алгоритмам классификации»