См. также: Прикладная математическая статистика (материалы к семинарам)
Измерительная техника. 2005. № 6. – С.13-19.
519.233.3:
006.91.001
Расширение области применения
критериев типа Граббса, используемых при отбраковке аномальных измерений
Б.Ю. Лемешко, С.Б. Лемешко
Получены таблицы процентных точек для статистик критериев типа Граббса при проверке на выброс одновременно трех максимальных (трех минимальных) значений и одновременно минимального и максимального значений в выборке. Методами статистического моделирования исследованы распределения статистик критериев Граббса, используемых в задачах отбраковки аномальных измерений, при отклонениях наблюдаемого закона от нормального.
Ключевые слова: проверка гипотез, аномальные наблюдения, критерии Граббса, процентные точки
Widening of
the application area of Grubbs’s tests used for screening of outlying
observations
B.Yu.
Lemeshko, S.B. Lemeshko
The tables of percentage points has been obtained
for Grubbs’s test statistics in case of testing for discards of three maximal
(or three minimal) values simultaneously or minimal and maximal values
simultaneously in a sample. The distributions of Grubbs’s test statistics have
been investigated by means of statistical simulation methods in problems of
screening of outlying observations in case of non-normal distribution under
observation.
Key words: testing
hypotheses, outlying observations, Grubbs’s tests, percentage points
В практической деятельности важную роль играют статистические критерии, предназначенные для выделения аномальных результатов измерений (выбросов). Если не исключить выбросы из анализируемых данных, то традиционно применяемые классические методы статистического анализа, как правило, не являющиеся робастными, чаще всего приводят к некорректным выводам.
Результаты измерений, содержащие грубые ошибки обычно бывают хорошо заметны и могут быть выделены без применения статистических методов. Применение статистических методов выявления грубых ошибок целесообразно лишь в сомнительных случаях, когда информация о качестве измерений либо неполна, либо ненадежна [1]. При этом, применяя статистические методы, следует отслеживать выполнение тех предположений, в условиях которых корректно их использование.
Большинство существующих критериев отбраковки “подозрительных” данных опирается на предположение о принадлежности наблюдаемых случайных величин нормальному закону. К такого рода критериям относятся простые критерии Граббса [2-4], применяемые для проверки на аномальность (для оценки анормальности) выделяющихся результатов измерений. Использование именно этих критериев предполагает стандарт [5], представляющий собой аутентичный текст соответствующего международного стандарта ИСО 5725. Статистики критерия Граббса предусматривают возможность проверки на наличие в выборке либо одного аномального результата измерения (наименьшего или наибольшего), либо двух (двух наименьших в выборке или двух наибольших).
Наш интерес к критериям Граббса был обусловлен предпочтением, отданным этим критериям при реализации стандарта ИСО 5725. В настоящей работе мы хотели показать, как изменяются распределения статистик критерия Граббса под влиянием отклонения наблюдаемого закона от нормального. Это должно дать понимание того, что будет происходить с результатами применения критериев при нарушении предположений о нормальности. Вторая цель заключалась в реализации возможности применения критериев с аналогичными статистиками для проверки еще двух гипотез: a) для проверки на аномальность одновременно одного минимального и одного максимального элементов в выборке; b) для проверки на аномальность либо трех минимальных, либо трех максимальных элементов в выборке.
В основе данных исследований лежит методика статистического моделирования, опирающаяся на развиваемое программное обеспечение.
Критерий Граббса проверки на один выброс. Пусть ![]() – наблюдаемая выборка,
– наблюдаемая выборка, ![]() – построенный по ней вариационный ряд. Проверяемая
гипотеза
– построенный по ней вариационный ряд. Проверяемая
гипотеза ![]() заключается в том, что все
заключается в том, что все ![]() принадлежат одной генеральной
совокупности. При проверке на выброс наибольшего выборочного значения
конкурирующая гипотеза
принадлежат одной генеральной
совокупности. При проверке на выброс наибольшего выборочного значения
конкурирующая гипотеза ![]() заключается в том, что
заключается в том, что ![]() принадлежат одному закону, а
принадлежат одному закону, а ![]() – некоторому другому,
существенно сдвинутому вправо. При проверке на выброс
– некоторому другому,
существенно сдвинутому вправо. При проверке на выброс ![]() статистика критерия Граббса имеет вид
статистика критерия Граббса имеет вид
где
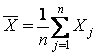 ,
(2)
,
(2)
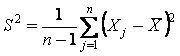 ,
(3)
,
(3)
![]() .
(4)
.
(4)
При проверке на выброс наименьшего выборочного
значения конкурирующая гипотеза ![]() предполагает, что
предполагает, что ![]() принадлежит некоторому другому
закону, существенно сдвинутому влево. В данном случае вычисляемая статистика
принимает вид
принадлежит некоторому другому
закону, существенно сдвинутому влево. В данном случае вычисляемая статистика
принимает вид
![]() .
(5)
.
(5)
Максимальный или минимальный элемент выборки считается
выбросом, если значение соответствующей статистики превысит критическое: ![]() или
или ![]() , где
, где ![]() – задаваемый уровень
значимости.
– задаваемый уровень
значимости.
Статистики (1) и (5) распределены одинаково. Вид
условных распределений ![]() статистик (1) и (5) в
зависимости от объема анализируемой выборки при нормальном законе
наблюдаемых величин представлен на рис. 1. Распределения статистики
существенно зависят от объема выборки
статистик (1) и (5) в
зависимости от объема анализируемой выборки при нормальном законе
наблюдаемых величин представлен на рис. 1. Распределения статистики
существенно зависят от объема выборки ![]() . Аналитический вид распределений статистики в стандарте [5]
и первоисточниках [2-4] не приводится. Даются лишь верхние процентные точки
для различных объемов выборок, так как решение об аномальности проверяемого
минимального или максимального выборочного значения принимается по правому
“хвосту” распределения статистики. Если в стандарте процентные точки
приведены для объемов выборок
. Аналитический вид распределений статистики в стандарте [5]
и первоисточниках [2-4] не приводится. Даются лишь верхние процентные точки
для различных объемов выборок, так как решение об аномальности проверяемого
минимального или максимального выборочного значения принимается по правому
“хвосту” распределения статистики. Если в стандарте процентные точки
приведены для объемов выборок ![]() лишь от 3 до 40, то в [4]
процентные точки приведены в диапазоне
лишь от 3 до 40, то в [4]
процентные точки приведены в диапазоне ![]() до 147.
до 147.
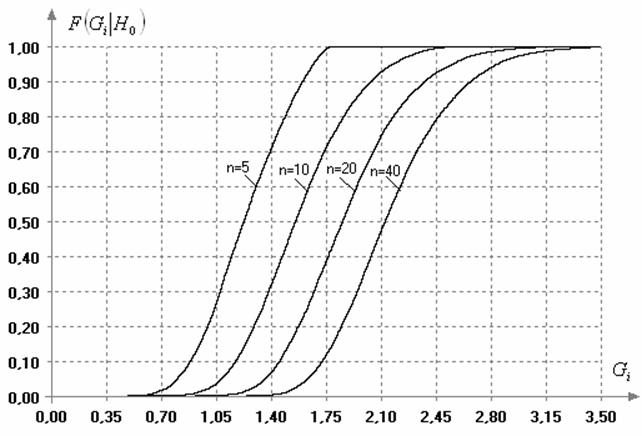
Рис. 1. Зависимость распределения
статистик (1) и (5) критерия Граббса от объема выборок ![]() (в случае нормального закона)
(в случае нормального закона)
Замечание: В таблице процентных точек, приведенной
в стандарте ([5], табл. 5), неверно указаны уровни значимости ![]() . На самом деле в данной таблице
представлены значения, соответствующие уровням значимости 0.005 (0.5%) и 0.025
(2.5%), а не 0.01 (1%) и 0.05 (5%). Чтобы убедиться в этом, достаточно
обратиться к первоисточнику [4]. Данное несоответствие было замечено в процессе
исследований распределений статистик Граббса. Это замечание в силе и для
процентных точек статистик, предназначенных для анализа на выбросы
одновременно двух минимальных или двух максимальных выборочных значений.
Вследствие такого недоразумения при задании уровня значимости 0.01 или 0.05 и
использовании процентных точек, приведенных в стандарте ([5], табл.5),
ошибочно не будет отбраковываться часть выбросов.
. На самом деле в данной таблице
представлены значения, соответствующие уровням значимости 0.005 (0.5%) и 0.025
(2.5%), а не 0.01 (1%) и 0.05 (5%). Чтобы убедиться в этом, достаточно
обратиться к первоисточнику [4]. Данное несоответствие было замечено в процессе
исследований распределений статистик Граббса. Это замечание в силе и для
процентных точек статистик, предназначенных для анализа на выбросы
одновременно двух минимальных или двух максимальных выборочных значений.
Вследствие такого недоразумения при задании уровня значимости 0.01 или 0.05 и
использовании процентных точек, приведенных в стандарте ([5], табл.5),
ошибочно не будет отбраковываться часть выбросов.
Данный критерий можно использовать
для выделения аномальных результатов измерений только в случае нормального
закона. Если наблюдаемые случайные величины принадлежат некоторому другому закону
распределения, то предельное распределение статистик (1) и (5) имеет иной вид.
На рис. 2 отражено изменение распределений статистик (1) и (5) в случае
принадлежности наблюдаемой случайной величины различным законам
экспоненциального семейства распределений с плотностью
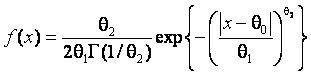 .
(6)
.
(6)
Частными случаями семейства являются
нормальный закон при параметре формы ![]() и распределение Лапласа при
и распределение Лапласа при ![]() . Предельными случаями – распределение Коши (
. Предельными случаями – распределение Коши (![]() ) и равномерное распределение (
) и равномерное распределение (![]() ). На рис. 2 приведены распределения статистик (1)
и (5) при наблюдаемых законах (6) со значениями параметра формы
). На рис. 2 приведены распределения статистик (1)
и (5) при наблюдаемых законах (6) со значениями параметра формы ![]() и при объемах выборок
и при объемах выборок ![]() . Как видим, распределения статистик
отличаются очень сильно.
. Как видим, распределения статистик
отличаются очень сильно.
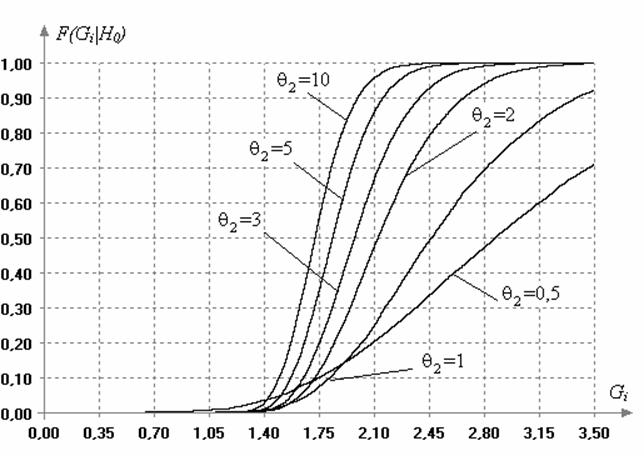
Рис.2. Изменение распределений статистик (1)
и (5) критерия Граббса в случае различных законов семейства распределений (6)
при ![]()
Справедливости ради следует напомнить, что впервые распределение статистики вида (1) было исследовано в работе [6]. В [1] приводится целый ряд статистик вида (1) и (5), отличающихся друг от друга комбинациями известных и оцениваемых параметров сдвига и масштаба нормального закона. Применение критериев, опирающихся на варианты таких статистик, было предусмотрено в [7, 8]. Все приводимые здесь статистики, не смотря на похожесть, отличаются от статистик Граббса (1) и (5), в которых используются оценки обоих параметров нормального закона. Вследствие этого и распределения ни одной из этих статистик не совпадает в точности с распределением статистик Граббса (1) и (5). Обзор еще ряда критериев, предназначенных для выявления и исключения аномальных выборочных значений, приведен в [9].
Проверка на два выброса. В этом случае конкурирующая гипотеза ![]() может быть связана с предположением,
что, например, некоторому другому закону принадлежат
может быть связана с предположением,
что, например, некоторому другому закону принадлежат ![]() и
и ![]() (либо
(либо ![]() и
и ![]() ). При проверке на выброс
одновременно двух наибольших значений статистика критерия Граббса имеет вид
). При проверке на выброс
одновременно двух наибольших значений статистика критерия Граббса имеет вид
![]() ,
(7)
,
(7)
где
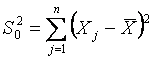 , (8)
, (8)
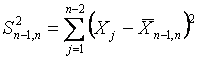 ,
(9)
,
(9)
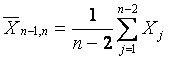 .
(10)
.
(10)
Для проверки на выброс одновременно двух наименьших
величин ![]() и
и ![]() статистика критерия принимает вид
статистика критерия принимает вид
![]() ,
(11)
,
(11)
где
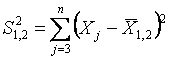 ,
(12)
,
(12)
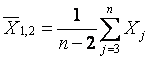 .
(13)
.
(13)
Оба значения (![]() ,
, ![]() или
или ![]() ,
, ![]() ) считаются выбросами, если значение
соответствующей статистики окажется ниже критического:
) считаются выбросами, если значение
соответствующей статистики окажется ниже критического: ![]() .
.
Вид условных распределений ![]() статистик
статистик ![]() (7) и (11) в зависимости от
объема анализируемой выборки представлен на рис. 3. Аналитический вид
распределений статистики
(7) и (11) в зависимости от
объема анализируемой выборки представлен на рис. 3. Аналитический вид
распределений статистики ![]() в стандарте [5] и в [2-4] не
приводится. Даются лишь нижние процентные точки для различных объемов выборок,
так как решение об аномальности одновременно двух наименьших или двух
наибольших выборочных значений принимается по левому “хвосту” распределения
статистики. В стандарте нижние процентные точки приведены для объемов выборок
в стандарте [5] и в [2-4] не
приводится. Даются лишь нижние процентные точки для различных объемов выборок,
так как решение об аномальности одновременно двух наименьших или двух
наибольших выборочных значений принимается по левому “хвосту” распределения
статистики. В стандарте нижние процентные точки приведены для объемов выборок ![]() лишь от 4 до 40. В первоисточнике
[4] нижние процентные точки распределения статистики
лишь от 4 до 40. В первоисточнике
[4] нижние процентные точки распределения статистики ![]() приведены в диапазоне
приведены в диапазоне ![]() до 149.
до 149.
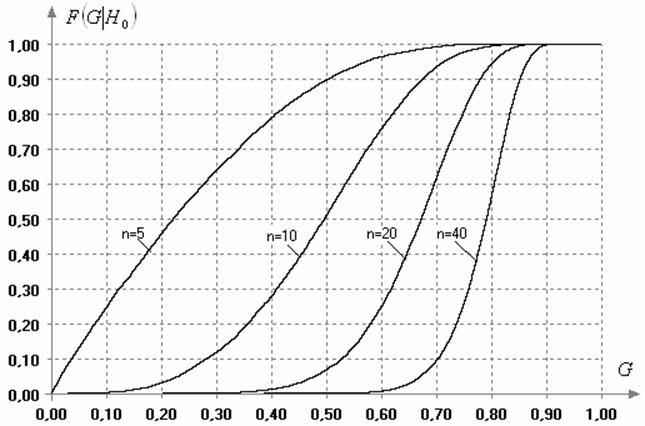
Рис. 3. Зависимость распределения статистик (7) и (11) критерия Граббса от объема выборок (в случае нормального закона)
Если наблюдаемые случайные величины принадлежат некоторому
другому закону, отличному от нормального, то распределения статистик (7) и (11)
принимают иной вид. Например, на рис. 4 приведены распределения статистик (7)
и (11) при наблюдаемых законах вида (6) со значениями параметра формы ![]() при объемах выборок
при объемах выборок ![]() . Как следует из картины,
представленной на этом рисунке, распределения статистик Граббса (7) и (11)
очень сильно зависят от вида закона, которому принадлежат наблюдаемые
величины.
. Как следует из картины,
представленной на этом рисунке, распределения статистик Граббса (7) и (11)
очень сильно зависят от вида закона, которому принадлежат наблюдаемые
величины.
Как и в первом случае, критерий со статистиками (7) – (11) можно применять для отбраковки аномальных наблюдений, используя таблицы процентных точек, приведенные в [5] и в [4], только в случае нормального закона. Если наблюдаемый закон отличается от нормального, то использование указанных таблиц, как следует из картин, представленных на рисунках 2 и 4, может приводить как к пропуску выбросов, так и к причислению к аномальным данных, не являющихся таковыми.
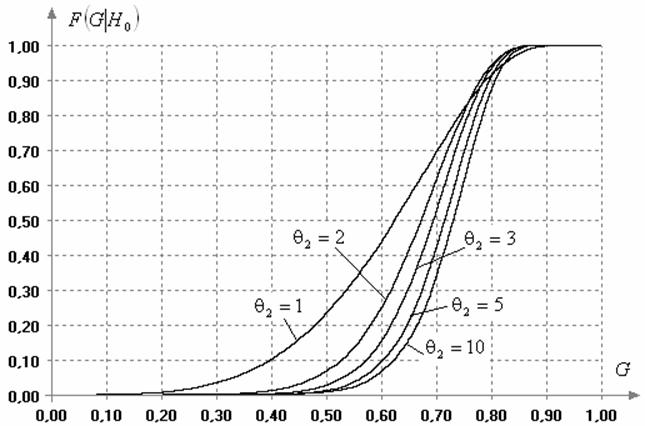
Рис. 4. Изменение распределений
статистик (7) и (11) Граббса в случае различных законов распределения при ![]()
Проверка на три выброса. Подход (7) – (13), можно естественно развивать для построения статистик, предназначенных, например, для проверки на аномальность одновременно трех минимальных или трех максимальных выборочных значений, или для проверки на выброс одновременно минимального и максимального значений в выборке. Для этого необходимо исследовать лишь распределения соответствующих статистик.
В случае проверки на
аномальность одновременно трех минимальных или трех максимальных выборочных
значений конкурирующая гипотеза ![]() предполагает, что некоторому
другому закону принадлежат
предполагает, что некоторому
другому закону принадлежат ![]() ,
, ![]() и
и ![]() (либо
(либо ![]() ,
, ![]() и
и ![]() ). Статистики для проверки на аномальность одновременно трех
минимальных или трех максимальных выборочных значений формируются в
соответствии с соотношениями:
). Статистики для проверки на аномальность одновременно трех
минимальных или трех максимальных выборочных значений формируются в
соответствии с соотношениями:
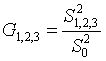 ,
(14)
,
(14)
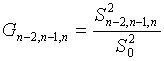 ,
(15)
,
(15)
где
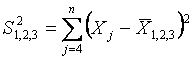 ,
(16)
,
(16)
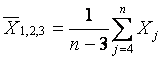 .
(17)
.
(17)
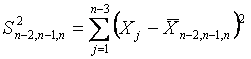 ,
(18)
,
(18)
 .
(19)
.
(19)
Статистики (14) и (15) распределены одинаково. Все три
измерения считаются выбросами, если значение соответствующей статистики окажется
ниже критического: ![]() или
или ![]() .
.
Естественно, что распределения данных
статистик также являются зависящими от объема выборок ![]() . На рис. 5 показана зависимость от
. На рис. 5 показана зависимость от ![]() условных распределений
условных распределений ![]() и
и ![]() статистик (14) и (15) в случае
извлечения выборок из нормальной генеральной совокупности. Вычисленные с
использованием методики статистического моделирования нижние процентные точки (
статистик (14) и (15) в случае
извлечения выборок из нормальной генеральной совокупности. Вычисленные с
использованием методики статистического моделирования нижние процентные точки (![]() =0.1%, 0.5%, 1%, 5%, 10%) распределений
статистик (14) и (15) при
=0.1%, 0.5%, 1%, 5%, 10%) распределений
статистик (14) и (15) при ![]() представлены в таблице 1. Процентные
точки строились по моделируемым выборкам статистик. Объем каждой выборки, по
которой оценивались процентные точки, составлял 50000 смоделированных
значений статистики. В таблице приведены значения процентных точек, полученные
усреднением по 15 таким экспериментам.
представлены в таблице 1. Процентные
точки строились по моделируемым выборкам статистик. Объем каждой выборки, по
которой оценивались процентные точки, составлял 50000 смоделированных
значений статистики. В таблице приведены значения процентных точек, полученные
усреднением по 15 таким экспериментам.
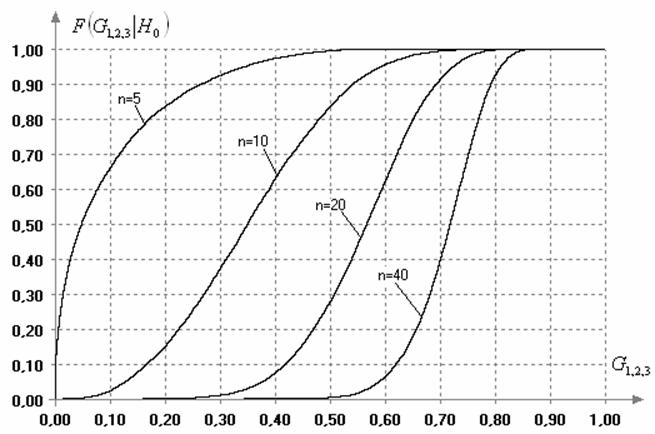
Рис. 5. Зависимость распределения статистик (14) и (15) от объема выборок (в случае нормального закона)
Таблица 1. Нижние процентные точки статистик (14) – (15) критерия типа Граббса
|
|
0.1% |
0.5% |
1% |
2.5% |
5% |
10% |
|
5 |
0.0000 |
0.0000 |
0.0000 |
0.0001 |
0.0004 |
0.0015 |
|
6 |
0.0002 |
0.0009 |
0.0019 |
0.0048 |
0.0099 |
0.0207 |
|
7 |
0.0023 |
0.0065 |
0.0106 |
0.0200 |
0.0332 |
0.0552 |
|
8 |
0.0079 |
0.0186 |
0.0268 |
0.0437 |
0.0640 |
0.0943 |
|
9 |
0.0176 |
0.0355 |
0.0478 |
0.0711 |
0.0966 |
0.1333 |
|
10 |
0.0314 |
0.0561 |
0.0717 |
0.1001 |
0.1302 |
0.1703 |
|
11 |
0.0471 |
0.0779 |
0.0968 |
0.1293 |
0.1619 |
0.2047 |
|
12 |
0.0659 |
0.1012 |
0.1222 |
0.1576 |
0.1925 |
0.2368 |
|
13 |
0.0841 |
0.1237 |
0.1471 |
0.1850 |
0.2206 |
0.2660 |
|
14 |
0.1035 |
0.1468 |
0.1707 |
0.2104 |
0.2475 |
0.2935 |
|
15 |
0.1234 |
0.1692 |
0.1943 |
0.2351 |
0.2726 |
0.3182 |
|
16 |
0.1412 |
0.1905 |
0.2170 |
0.2583 |
0.2962 |
0.3419 |
|
17 |
0.1607 |
0.2109 |
0.2374 |
0.2799 |
0.3178 |
0.3631 |
|
18 |
0.1797 |
0.2309 |
0.2583 |
0.3008 |
0.3382 |
0.3828 |
|
19 |
0.1973 |
0.2503 |
0.2782 |
0.3197 |
0.3575 |
0.4016 |
|
20 |
0.2161 |
0.2688 |
0.2966 |
0.3387 |
0.3757 |
0.4190 |
|
21 |
0.2313 |
0.2856 |
0.3139 |
0.3558 |
0.3924 |
0.4348 |
|
22 |
0.2488 |
0.3023 |
0.3303 |
0.3718 |
0.4082 |
0.4505 |
|
23 |
0.2643 |
0.3197 |
0.3466 |
0.3881 |
0.4238 |
0.4645 |
|
24 |
0.2795 |
0.3339 |
0.3606 |
0.4020 |
0.4375 |
0.4782 |
|
25 |
0.2952 |
0.3491 |
0.3762 |
0.4164 |
0.4510 |
0.4906 |
|
26 |
0.3091 |
0.3625 |
0.3890 |
0.4294 |
0.4638 |
0.5028 |
|
27 |
0.3209 |
0.3750 |
0.4022 |
0.4415 |
0.4756 |
0.5144 |
|
28 |
0.3357 |
0.3887 |
0.4151 |
0.4536 |
0.4874 |
0.5250 |
|
29 |
0.3475 |
0.4001 |
0.4270 |
0.4658 |
0.4984 |
0.5353 |
|
30 |
0.3608 |
0.4127 |
0.4382 |
0.4763 |
0.5087 |
0.5451 |
|
31 |
0.3710 |
0.4228 |
0.4486 |
0.4867 |
0.5186 |
0.5544 |
|
32 |
0.3797 |
0.4331 |
0.4596 |
0.4968 |
0.5282 |
0.5634 |
|
33 |
0.3935 |
0.4441 |
0.4692 |
0.5060 |
0.5370 |
0.5716 |
|
34 |
0.4040 |
0.4547 |
0.4793 |
0.5151 |
0.5456 |
0.5798 |
|
35 |
0.4131 |
0.4643 |
0.4885 |
0.5242 |
0.5541 |
0.5876 |
|
36 |
0.4239 |
0.4730 |
0.4974 |
0.5330 |
0.5623 |
0.5952 |
|
37 |
0.4317 |
0.4824 |
0.5064 |
0.5411 |
0.5697 |
0.6023 |
|
38 |
0.4414 |
0.4915 |
0.5149 |
0.5487 |
0.5772 |
0.6090 |
|
39 |
0.4511 |
0.4999 |
0.5228 |
0.5563 |
0.5843 |
0.6158 |
|
40 |
0.4610 |
0.5077 |
0.5296 |
0.5630 |
0.5910 |
0.6219 |
|
41 |
0.4667 |
0.5146 |
0.5381 |
0.5706 |
0.5978 |
0.6279 |
|
42 |
0.4751 |
0.5226 |
0.5452 |
0.5774 |
0.6041 |
0.6338 |
|
43 |
0.4839 |
0.5299 |
0.5517 |
0.5836 |
0.6102 |
0.6397 |
|
44 |
0.4910 |
0.5366 |
0.5585 |
0.5899 |
0.6159 |
0.6450 |
|
45 |
0.4997 |
0.5436 |
0.5651 |
0.5960 |
0.6217 |
0.6504 |
|
46 |
0.5057 |
0.5498 |
0.5713 |
0.6020 |
0.6274 |
0.6553 |
|
47 |
0.5131 |
0.5562 |
0.5775 |
0.6075 |
0.6327 |
0.6605 |
|
48 |
0.5191 |
0.5622 |
0.5833 |
0.6131 |
0.6380 |
0.6653 |
|
49 |
0.5247 |
0.5684 |
0.5891 |
0.6183 |
0.6430 |
0.6698 |
|
50 |
0.5316 |
0.5745 |
0.5947 |
0.6239 |
0.6477 |
0.6743 |
Распределения статистик (14) – (15) также зависят от
наблюдаемого закона. Рис. 6 иллюстрирует поведение распределений данных статистик
при наблюдаемых законах вида (6) со значениями параметра формы ![]() при объемах выборок
при объемах выборок ![]() .
.
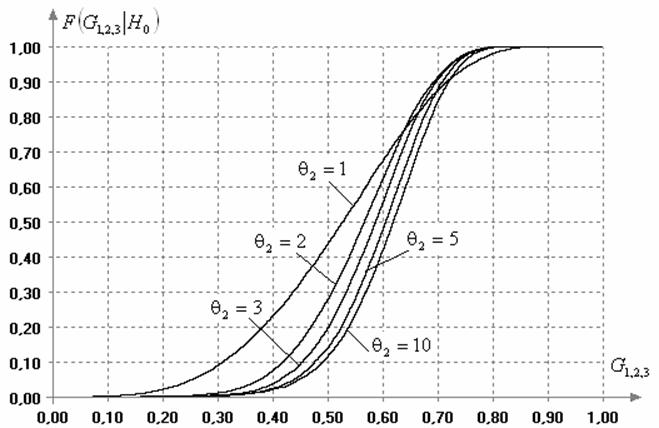
Рис. 6. Изменение распределений
статистик (14) и (15) в случае различных законов семейства распределений (6)
при ![]()
Одновременная проверка на выброс наименьшего и наибольшего
значения. Статистика для
проверки на аномальность одновременно минимального и максимального
выборочных значений формируется в соответствии с соотношением:
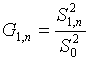 ,
(20)
,
(20)
где
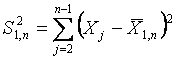 ,
(21)
,
(21)
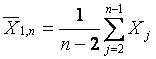 .
(22)
.
(22)
Оба значения считаются выбросами при заданном уровне
значимости ![]() , если вычисленное по выборке
значение статистики (20) окажется ниже критического:
, если вычисленное по выборке
значение статистики (20) окажется ниже критического: ![]() .
.
Вид условных распределений ![]() статистики (20)
статистики (20) ![]() в зависимости от объема
в зависимости от объема ![]() в случае извлечения анализируемой выборки из нормальной
генеральной совокупности представлен на рис. 7. Вычисленные с использованием
методики статистического моделирования нижние процентные точки распределений
статистики (14) при
в случае извлечения анализируемой выборки из нормальной
генеральной совокупности представлен на рис. 7. Вычисленные с использованием
методики статистического моделирования нижние процентные точки распределений
статистики (14) при ![]() приведены в таблице 2.
приведены в таблице 2.
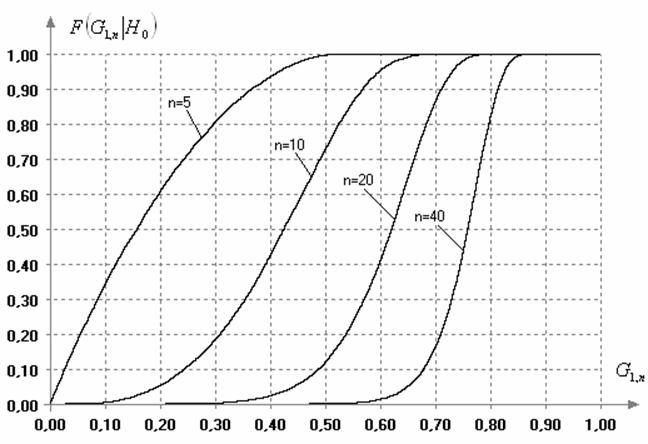
Рис. 7. Зависимость распределения статистики (20) от объема выборки (в случае нормального закона)
Таблица 2. Нижние процентные точки статистик (20) критерия типа Граббса
|
|
0.1% |
0.5% |
1% |
2.5% |
5% |
10% |
|
5 |
0.0003 |
0.0012 |
0.0025 |
0.0063 |
0.0129 |
0.0265 |
|
6 |
0.0030 |
0.0089 |
0.0140 |
0.0262 |
0.0427 |
0.0698 |
|
7 |
0.0110 |
0.0243 |
0.0349 |
0.0562 |
0.0809 |
0.1178 |
|
8 |
0.0242 |
0.0468 |
0.0620 |
0.0908 |
0.1218 |
0.1644 |
|
9 |
0.0408 |
0.0712 |
0.0908 |
0.1252 |
0.1608 |
0.2073 |
|
10 |
0.0610 |
0.0991 |
0.1215 |
0.1606 |
0.1981 |
0.2464 |
|
11 |
0.0845 |
0.1279 |
0.1529 |
0.1939 |
0.2334 |
0.2821 |
|
12 |
0.1072 |
0.1544 |
0.1813 |
0.2247 |
0.2648 |
0.3135 |
|
13 |
0.1307 |
0.1813 |
0.2091 |
0.2538 |
0.2948 |
0.3428 |
|
14 |
0.1527 |
0.2065 |
0.2356 |
0.2808 |
0.3219 |
0.3696 |
|
15 |
0.1747 |
0.2313 |
0.2605 |
0.3059 |
0.3463 |
0.3936 |
|
16 |
0.1964 |
0.2537 |
0.2837 |
0.3291 |
0.3697 |
0.4160 |
|
17 |
0.2162 |
0.2756 |
0.3052 |
0.3512 |
0.3907 |
0.4367 |
|
18 |
0.2357 |
0.2969 |
0.3268 |
0.3718 |
0.4110 |
0.4556 |
|
19 |
0.2571 |
0.3164 |
0.3465 |
0.3912 |
0.4298 |
0.4730 |
|
20 |
0.2762 |
0.3358 |
0.3650 |
0.4094 |
0.4474 |
0.4895 |
|
21 |
0.2950 |
0.3543 |
0.3829 |
0.4264 |
0.4636 |
0.5051 |
|
22 |
0.3114 |
0.3702 |
0.3994 |
0.4424 |
0.4787 |
0.5191 |
|
23 |
0.3268 |
0.3864 |
0.4154 |
0.4573 |
0.4932 |
0.5326 |
|
24 |
0.3448 |
0.4013 |
0.4297 |
0.4714 |
0.5064 |
0.5451 |
|
25 |
0.3590 |
0.4153 |
0.4440 |
0.4848 |
0.5187 |
0.5567 |
|
26 |
0.3732 |
0.4294 |
0.4576 |
0.4973 |
0.5310 |
0.5679 |
|
27 |
0.3865 |
0.4423 |
0.4699 |
0.5097 |
0.5422 |
0.5784 |
|
28 |
0.3994 |
0.4547 |
0.4818 |
0.5208 |
0.5529 |
0.5884 |
|
29 |
0.4133 |
0.4673 |
0.4930 |
0.5317 |
0.5631 |
0.5978 |
|
30 |
0.4257 |
0.4791 |
0.5050 |
0.5422 |
0.5731 |
0.6067 |
|
31 |
0.4376 |
0.4885 |
0.5145 |
0.5511 |
0.5819 |
0.6152 |
|
32 |
0.4477 |
0.4995 |
0.5249 |
0.5608 |
0.5908 |
0.6235 |
|
33 |
0.4558 |
0.5099 |
0.5346 |
0.5702 |
0.5993 |
0.6314 |
|
34 |
0.4688 |
0.5189 |
0.5431 |
0.5783 |
0.6072 |
0.6384 |
|
35 |
0.4779 |
0.5285 |
0.5524 |
0.5864 |
0.6149 |
0.6456 |
|
36 |
0.4874 |
0.5374 |
0.5612 |
0.5946 |
0.6225 |
0.6525 |
|
37 |
0.4970 |
0.5459 |
0.5688 |
0.6022 |
0.6296 |
0.6591 |
|
38 |
0.5048 |
0.5540 |
0.5767 |
0.6091 |
0.6359 |
0.6652 |
|
39 |
0.5145 |
0.5617 |
0.5839 |
0.6166 |
0.6425 |
0.6711 |
|
40 |
0.5211 |
0.5692 |
0.5917 |
0.6229 |
0.6489 |
0.6768 |
|
41 |
0.5307 |
0.5767 |
0.5985 |
0.6295 |
0.6548 |
0.6823 |
|
42 |
0.5385 |
0.5835 |
0.6052 |
0.6360 |
0.6606 |
0.6877 |
|
43 |
0.5450 |
0.5902 |
0.6117 |
0.6417 |
0.6662 |
0.6928 |
|
44 |
0.5522 |
0.5970 |
0.6181 |
0.6476 |
0.6715 |
0.6977 |
|
45 |
0.5599 |
0.6033 |
0.6237 |
0.6529 |
0.6767 |
0.7025 |
|
46 |
0.5675 |
0.6090 |
0.6295 |
0.6582 |
0.6817 |
0.7071 |
|
47 |
0.5742 |
0.6154 |
0.6356 |
0.6637 |
0.6865 |
0.7115 |
|
48 |
0.5789 |
0.6211 |
0.6412 |
0.6687 |
0.6913 |
0.7159 |
|
49 |
0.5861 |
0.6270 |
0.6461 |
0.6733 |
0.6957 |
0.7200 |
|
50 |
0.5910 |
0.6324 |
0.6512 |
0.6783 |
0.7002 |
0.7240 |
Распределения статистики (20) существенно зависят от
наблюдаемого закона. Рис. 8 показывает, как меняются распределения данной статистики
при наблюдаемых законах вида (6) со значениями параметра формы ![]() при объемах выборок
при объемах выборок ![]() .
.
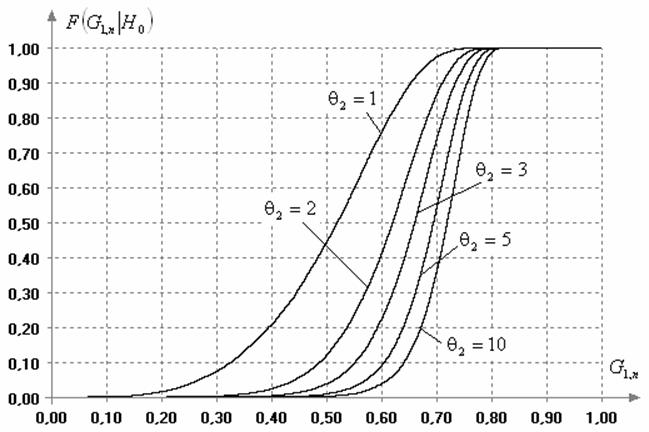
Рис. 8. Изменение распределений
статистики (20) в случае различных законов семейства распределений (6) при ![]()
Каждый из рассмотренных критериев позволяет (способен) отбраковывать содержащиеся в выборке аномальные данные, если количество выбросов в выборке не превышает их числа, на которое рассчитан соответствующий критерий. В тех случаях, когда используемый критерий соответствует “реальному числу” выбросов, последние, как правило, удается выделить с применением этого критерия. При содержании в выборке большего числа грубых ошибок измерений, чем предусматривает статистика, критерий уже не способен их выделять. Например, если проверка на выброс одного наибольшего значения не дала положительного результата, это еще не означает, что данное значение не является выбросом. Возможно, что в выборке содержится больше значений, которые могут интерпретироваться как аномальные. Присутствие таких данных отражается на оценках дисперсии (3), (8), и оценках характеристик рассеяния (9), (12), (16), (18), (21), так как все они не являются робастными. Следовательно, при использовании критериев типа Граббса необходимо последовательно тестировать выборку на наличие различного числа грубых ошибок измерений.
Выбросы в результатах измерений могут быть вызваны появлением “сдвинутых” значений, связанных с систематической ошибкой, могут быть связаны с увеличением рассеяния результатов измерений в силу различных причин. В последнем случае к выбросам могут относиться как наименьшие, так и наибольшие значения. Способность рассмотренных критериев выделять аномальные результаты измерений будет зависеть от вида засорения.
В качестве примера
покажем мощность критериев на модели с симметричным засорением, кода выборка из
нормальной генеральной совокупности с параметром сдвига ![]() и параметром масштаба
и параметром масштаба ![]() засорена 10% наблюдений
нормального закона с параметрами
засорена 10% наблюдений
нормального закона с параметрами ![]() и 5
и 5![]() :
:
![]() .
.
Мощность критерия
при заданной вероятности ![]() ошибки первого рода определяется
величиной
ошибки первого рода определяется
величиной ![]() , где
, где ![]() – вероятность ошибки второго рода. В данном случае
ошибка второго рода заключается в том, что аномальное значение не
идентифицируется как таковое. В таблице 3 приведены мощности критериев
проверки на аномальность одного минимального (или максимального) значения в
выборке, одновременно двух минимальных (двух максимальных) значений,
одновременно одного минимального и одного максимального значений в выборке
объемом
– вероятность ошибки второго рода. В данном случае
ошибка второго рода заключается в том, что аномальное значение не
идентифицируется как таковое. В таблице 3 приведены мощности критериев
проверки на аномальность одного минимального (или максимального) значения в
выборке, одновременно двух минимальных (двух максимальных) значений,
одновременно одного минимального и одного максимального значений в выборке
объемом ![]() . Более высокая в данном случае
мощность критерия со статистикой (20) объясняется симметричностью засорения.
. Более высокая в данном случае
мощность критерия со статистикой (20) объясняется симметричностью засорения.
Таблица 3. Значения мощности ![]() критериев типа Граббса по
отношению к смеси с 10% симметричным засорением при
критериев типа Граббса по
отношению к смеси с 10% симметричным засорением при ![]()
|
Уровень
значимости |
Мощность критерия |
||
|
со статистикой (1) и (5) |
со статистикой (7) и (11) |
со статистикой (20) |
|
|
0.10 |
0.3763 |
0.3586 |
0.6094 |
|
0.05 |
0.3285 |
0.3115 |
0.5448 |
|
0.01 |
0.2431 |
0.2351 |
0.4164 |
Параметрическая отбраковка наблюдений. Таблицы процентных точек критериев Граббса, полученные в [2-4], сокращенная таблица, приведенная в [5], расширения критерия, рассмотренные в данной работе, и построенные здесь таблицы соответствующих процентных точек позволяют корректно отбраковывать грубые ошибки измерений (выбросы) в случае выполнения предположения о нормальности наблюдаемого закона. Если предположения о нормальности нарушаются, использовать указанные таблицы процентных точек нельзя. Как показано выше, распределения статистик критериев типа Граббса существенно зависят от истинного закона распределения наблюдаемой случайной величины.
Вообще говоря, в случае необходимости нет принципиальных трудностей для построения модели распределения любой рассмотренной статистики критерия типа Граббса (или для определения процентных точек) при любом законе наблюдаемых случайных величин. Проблема лишь в том, что законов, для которых желательно иметь эффективную процедуру отбраковки аномальных измерений, слишком много.
Логичней при анализе
данных на аномальность опираться на “истинный” закон распределения
наблюдаемой величины. В этом случае задача отбраковки, формулируется следующим
образом. Проверяемая гипотеза ![]() заключается в том, что все
заключается в том, что все ![]() принадлежат одной генеральной
совокупности с законом распределения
принадлежат одной генеральной
совокупности с законом распределения ![]() . При проверке на выброс наибольшего
выборочного значения
. При проверке на выброс наибольшего
выборочного значения ![]() конкурирующая гипотеза
конкурирующая гипотеза ![]() заключается в том, что
заключается в том, что ![]() принадлежат
принадлежат ![]() , а
, а ![]() – некоторому распределению
– некоторому распределению ![]() , которое “существенно сдвинуто вправо” относительно
, которое “существенно сдвинуто вправо” относительно ![]() , например,
, например, ![]() , где
, где ![]() достаточно велико. Если
достаточно велико. Если ![]() , то принимается гипотеза
, то принимается гипотеза ![]() , в противном случае - гипотеза
, в противном случае - гипотеза ![]() . При справедливости нулевой гипотезы
. При справедливости нулевой гипотезы
![]() , и критическое значение определяется
из уравнения
, и критическое значение определяется
из уравнения ![]() .
.
При проверке на выброс наименьшего значения ![]() гипотеза
гипотеза ![]() принимается, если
принимается, если ![]() . В этом случае
. В этом случае ![]() , и критическое значение определяется
из уравнения
, и критическое значение определяется
из уравнения ![]() .
.
Чтобы с помощью данной
процедуры корректно выделять содержащиеся в выборке грубые ошибки, необходимо
знание “истинного” закона ![]() . Однако на практике вектор
параметров
. Однако на практике вектор
параметров ![]() закона
закона ![]() чаще всего приходится оценивать по этой же самой
выборке. В связи с чем такую процедуру отбраковки иногда называют параметрической.
Содержащиеся в выборке выбросы отражаются на оценках параметров закона
чаще всего приходится оценивать по этой же самой
выборке. В связи с чем такую процедуру отбраковки иногда называют параметрической.
Содержащиеся в выборке выбросы отражаются на оценках параметров закона ![]() . Полученный закон
. Полученный закон ![]() оказывается существенно
отличающимся от “истинного”. Вследствие этого параметрические методы отбраковки
резко выделяющихся наблюдений становятся неустойчивыми [10].
оказывается существенно
отличающимся от “истинного”. Вследствие этого параметрические методы отбраковки
резко выделяющихся наблюдений становятся неустойчивыми [10].
Следует отметить, что подобным же недостатком обладают и критерии типа Граббса: нет никакой гарантии, что в выборке не большее число аномальных измерений, чем мы исследуем на выбросы. Тогда это может отрицательно сказаться на результатах анализа.
В параметрических методах отбраковки с данным недостатком борются, применяя робастные методы оценивания, например, оценки максимального правдоподобия по группированным данным [11], оптимальные L-оценки по выборочным квантилям [12, 13], MD-оценки. Использование робастных методов оценивания в процедуре параметрической отбраковки делает ее очень эффективной [11].
Робастные методы оценивания математического ожидания и среднего квадратичного отклонения можно использовать и при вычислении статистик критериев типа Граббса. Однако в этом случае обязательно следует учитывать, что метод оценивания отразится на распределениях статистик.
Таблицы построенных
процентных точек, расширенные для объемов выборок до ![]() , доступны по адресу http:\\www.ami.nstu.ru\ ~headrd\seminar\start.htm.
, доступны по адресу http:\\www.ami.nstu.ru\ ~headrd\seminar\start.htm.
Работа выполнена при финансовой поддержке Минобразования РФ (проект № ТО2-3.3-3356)
Литература
1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
2. Frank
E. Grubbs. Sample Criteria for Testing Outlying observations // Ann. Math.
Statist, 1950. – Vol. 21. – No. 1. – P.27-58.
3. Frank
E. Grubbs. Procedures for Detecting Outlying Observations
in Samples // Technometrics, 1969. – Vol. 11. – No. 1. – P.1-21
4. Frank E. Grubbs, Glenn Beck. Extension of sample sizes and percentage points for significance tests of outlying observations // Technometrics, 1972. – Vol. 14. – No. 4. – P.847-854.
5. ГОСТ Р ИСО 5725-2–2002. Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. М.: Изд-во стандартов. – 51 с.
6. Смирнов Н.В. Оценка максимального члена в ряду наблюдений // Доклады АН СССР, 1941. – Т. 33. – № 5. – С. 346-349.
7. ГОСТ 11.002-73. Прикладная статистика. Правила оценки анормальности результатов наблюдений. М.: Изд-во стандартов. 1982. – 26 с.
8. СТ СЭВ 545-77. Прикладная статистика. Правила оценки анормальности результатов наблюдений. М.: Изд-во стандартов. 1978. – 26 с.
9. Микешина Н.Г. Выявление и исключение аномальных значений // Заводская лаборатория. 1966. – Т. 22. – № 3. – С. 310-318.
10. Орлов А.И. Неустойчивость параметрических методов отбраковки резко выделяющихся наблюдений // Заводская лаборатория. 1992. – Т. 58. – № 7. – С. 40-42.
11. Лемешко Б.Ю. Робастные методы оценивания и отбраковка аномальных измерений // Заводская лаборатория. – 1997. – Т.63. – № 5. – С. 43-49.
12. Лемешко Б.Ю., Чимитова Е.В. Построение оптимальных L-оценок параметров сдвига и масштаба распределений по выборочным квантилям // Сибирский журнал индустриальной математики. 2001. – Т.4. – № 2. – С. 166-183.
13. Лемешко Б.Ю., Чимитова Е.В. Оптимальные L-оценки параметров сдвига и масштаба распределений по выборочным квантилям // Заводская лаборатория. Диагностика материалов. 2004. – Т.70. – № 1. – С. 54-66.